Advertisements
Advertisements
प्रश्न
A 12 metre tall tree was broken into two parts. It was found that the height of the part which was left standing was the cube root of the length of the part that was cut away. Formulate this into a mathematical problem to find the height of the part which was left standing
उत्तर
Let the height of the tree = 12
Length of the cut part = x3
Length of left out part = `root(3)(x^3)`
= x
Given x + x3 = 12
x3 + x – 12 = 0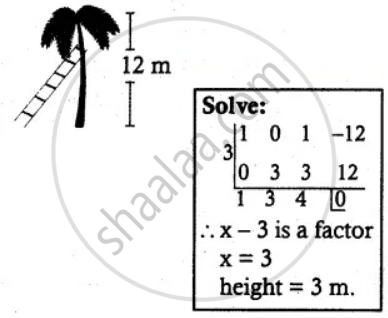
Which is required mathematical problem
APPEARS IN
संबंधित प्रश्न
Construct a cubic equation with roots 1, 2 and 3
Construct a cubic equation with roots 1, 1, and – 2
If α, β and γ are the roots of the cubic equation x3 + 2x2 + 3x + 4 = 0, form a cubic equation whose roots are 2α, 2β, 2γ
If α, β and γ are the roots of the cubic equation x3 + 2x2 + 3x + 4 = 0, form a cubic equation whose roots are `1/alpha, 1/beta, 1/γ`
If α, β and γ are the roots of the cubic equation x3 + 2x2 + 3x + 4 = 0, form a cubic equation whose roots are `- alpha, -beta, -γ`
Solve the equation 3x3 – 16x2 + 23x – 6 = 0 if the product of two roots is 1
Find the sum of squares of roots of the equation `2x^4 - 8x^3 + 6x^2 - 3` = 0
Solve the equation x3 – 9x2 + 14x + 24 = 0 if it is given that two of its roots are in the ratio 3 : 2
If α, β, and γ are the roots of the polynomial equation ax3 + bx2 + cx + d = 0, find the value of `sum alpha/(betaγ)` in terms of the coefficients
If α, β, γ and δ are the roots of the polynomial equation 2x4 + 5x3 – 7x2 + 8 = 0, find a quadratic equation with integer coefficients whose roots are α + β + γ + δ and αβγδ
If p and q are the roots of the equation lx2 + nx + n = 0, show that `sqrt("p"/"q") + sqrt("q"/"p") + sqrt("n"/l)` = 0
If the equations x2 + px + q = 0 and x2 + p’x + q’ = 0 have a common root, show that it must be equal to `("pq'" - "p'q")/("q" - "q")` or `("q" - "q'")/("p'" - "P")`
