Advertisements
Advertisements
प्रश्न
A 5.5 m long ladder is leaned against a wall. The ladder reaches the wall to a height of 4.4 m. Find the distance between the wall and the foot of the ladder.
उत्तर
Let the distance between the wall and the foot of the ladder be x m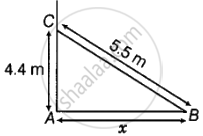
In right-angled ΔABC, by using Pythagoras theorem, we get
BC2 = AB2 + AC2
⇒ (5.5)2 = x2 + (4.4)2
⇒ x2 = (5.5)2 – (4.4)2
⇒ x2 = 30.25 – 19.36
⇒ x2 = 10.89
⇒ x = `sqrt(10.89)`
| 3.3 | |
| 3 | `bar10.bar89` |
| 9 | |
| 63 | 189 |
| 189 | |
| 0 |
∴ x = 3.3 m
Hence, the distance between the wall and the foot of the ladder is 3.3 m.
APPEARS IN
संबंधित प्रश्न
What will be the units digit of the square of the following number?
4583
What will be the units digit of the square of the following number?
78367
Which of the following triplet pythagorean?
(12, 35, 38)
Observe the following pattern
\[\left( 1 \times 2 \right) + \left( 2 \times 3 \right) = \frac{2 \times 3 \times 4}{3}\]
\[\left( 1 \times 2 \right) + \left( 2 \times 3 \right) + \left( 3 \times 4 \right) = \frac{3 \times 4 \times 5}{3}\]
\[\left( 1 \times 2 \right) + \left( 2 \times 3 \right) + \left( 3 \times 4 \right) + \left( 4 \times 5 \right) = \frac{4 \times 5 \times 6}{3}\]
and find the value of(1 × 2) + (2 × 3) + (3 × 4) + (4 × 5) + (5 × 6)
Observe the following pattern \[1^2 = \frac{1}{6}\left[ 1 \times \left( 1 + 1 \right) \times \left( 2 \times 1 + 1 \right) \right]\]
\[ 1^2 + 2^2 = \frac{1}{6}\left[ 2 \times \left( 2 + 1 \right) \times \left( 2 \times 2 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 = \frac{1}{6}\left[ 3 \times \left( 3 + 1 \right) \times \left( 2 \times 3 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 + 4^2 = \frac{1}{6}\left[ 4 \times \left( 4 + 1 \right) \times \left( 2 \times 4 + 1 \right) \right]\] and find the values :
52 + 62 + 72 + 82 + 92 + 102 + 112 + 122
Find the square of the following number:
503
Find a Pythagorean triplet in which one member is 12.
The hypotenuse of a right triangle with its legs of lengths 3x × 4x is ______.
For every natural number m, (2m – 1, 2m2 – 2m, 2m2 – 2m + 1) is a pythagorean triplet.
Find the length of the side of a square if the length of its diagonal is 10 cm.
