Advertisements
Advertisements
प्रश्न
A(6,1) , B(8,2) and C(9,4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE
उत्तर
Let (x,y) be the coordinates of D and ( x ',y')be thee coordinates of E. since, the diagonals of a parallelogram bisect each other at the same point, therefore
`(x+8)/2=(6+9)/2⇒x =7`
`(y+2)/2 = (1+4)/2 ⇒ y=3`
Thus, the coordinates of D are ( 7,3)
E is the midpoint of DC, therefore
`x' = (7+9)/2 ⇒ x' = 8`
`y' =(3+4)/2 ⇒ y' = 7/2 `
Thus, the coordinates of E are `(8,7/2)`
`"let" A (x_1, y_1) = A(6,1) ,E (x_2,y_2) = E (8,7/2) and D(x_3,y_3) = D(7,3) Now`
`"Area" (Δ ABC) = 1/2 [ x_1(y_2-y_3)+x_2(y_3-y_1) +x_3(y_1-y_2)]`
`=1/2[6(7/2-3)+8(3-1)+7(1-7/2)]`
`=1/2[3/2]`
`=3/4` sq. units
Hence, the area of the triangle ΔADE is `3/ 4`sq. units
APPEARS IN
संबंधित प्रश्न
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find the area of the following triangle:
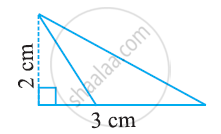
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
Using determinants, find the values of k, if the area of triangle with vertices (–2, 0), (0, 4) and (0, k) is 4 square units.
In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
Ratio of the area of ∆WXY to the area of ∆WZY is 3:4 in the given figure. If the area of ∆WXZ is 56 cm2 and WY = 8 cm, find the lengths of XY and YZ.

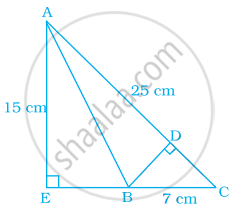
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.