Advertisements
Advertisements
प्रश्न
A bar magnet has a length of 8 cm. The magnetic field at a point at a distance 3 cm from the centre in the broadside-on position is found to be `4 xx 10^-6 "T"`.Find the pole strength of the magnet.
उत्तर
Given:
Length of the magnet, 2l = 8 cm = `8 xx 10^-2 "m"`
Distance of the observation point from the centre of the dipole, d = 3 cm
Magnetic field in the broadside-on position, B = `4 xx 10^-6 "T"`
The magnetic field due to the dipole on the equatorial point (B) is given by
`B = (u_0m2l)/(4pi(d^2 + l^2)^(3/2)`
Here, m is the pole strength of the magnet.
On substituting the respective values, we get
`4 xx 10^-6 = (10^-7"m" xx 8 xx 10^-2)/(9 xx 10^-4 + 16 xx 10^-4)^(3/2)`
⇒ `4 xx 10^-6 = ("m" xx 8 xx 10^-9)/((25)^(3/2) xx (10^-4)^(3/2)`
⇒ `"m" = (4 xx 10^-6 xx 125 xx 10^-6)/(8 xx 10^-9)`
⇒ `"m" = 6.25 xx 10^-2 "A-m"`
APPEARS IN
संबंधित प्रश्न
State how magnetic susceptibility is different for the three types of magnetic materials, i.e. diamagnetic, paramagnetic and ferromagnetic materials
State two advantages of an electromagnet over a permanent magnet.
The force on a north pole, `vecF = mvecB` , parallel to the field `vecB` . Does it contradict our earlier knowledge that a magnetic field can exert forces only perpendicular to itself?
Magnetic scalar potential is defined as `U(vec r_2) - U(vec r_1) = - ∫_vec(r_1)^vec(r_2)` `vec (B) . dvec(l)`
Apply this equation to a closed curve enclosing a long straight wire. The RHS of the above equation is then `-u_0 i` by Ampere's law. We see that `U(vec(r_2)) ≠ U(vec(r_1))` even when `vec r_2 =vec r_1` .Can we have a magnetic scalar potential in this case?
A dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay ______.
A very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying as electric current i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
Consider the situation of the previous problem. The directions of the magnetic field due to the dipole are opposite at
(a) P1 and P2
(b) Q1 and Q2
(c) P1 and Q1
(d) P2 and Q2
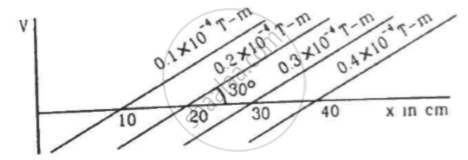
Figure shows some of the equipotential surfaces of the magnetic scalar potential. Find the magnetic field B at a point in the region.
Show that the magnetic field at a point due to a magnetic dipole is perpendicular to the magnetic axis if the line joining the point with the centre of the dipole makes an angle of `tan^-1(sqrt 2)` with the magnetic axis
Why is it not possible to make permanent magnets from paramagnetic materials?
The coercive force for a certain permanent magnet is 4.0 × 104 A m−1. This magnet is placed inside a long solenoid of 40 turns/cm and a current is passed in the solenoid to demagnetise it completely. Find the current.
The magnetic field due to the earth has a horizontal component of 26 μT at a place where the dip is 60°. Find the vertical component and the magnitude of the field.
The needle of a dip circle shows an apparent dip of 45° in a particular position and 53° when the circle is rotated through 90°. Find the true dip.
A moving-coil galvanometer has a 50-turn coil of size 2 cm × 2 cm. It is suspended between the magnetic poles producing a magnetic field of 0.5 T. Find the torque on the coil due to the magnetic field when a current of 20 mA passes through it.
A short magnet produces a deflection of 37° in a deflection magnetometer in Tan-A position when placed at a separation of 10 cm from the needle. Find the ratio of the magnetic moment of the magnet to the earth's horizontal magnetic field.
The magnetometer of the previous problem is used with the same magnet in Tan-B position. Where should the magnet be placed to produce a 37° deflection of the needle?
The combination of two bar magnets makes 10 oscillations per second in an oscillation magnetometer when like poles are tied together and 2 oscillations per second when unlike poles are tied together. Find the ratio of the magnetic moments of the magnets. Neglect any induced magnetism.
A bar magnet makes 40 oscillations per minute in an oscillation magnetometer. An identical magnet is demagnetized completely and is placed over the magnet in the magnetometer. Find the time taken for 40 oscillations by this combination. Neglect any induced magnetism.
A short magnet makes 40 oscillations per minute when used in an oscillation magnetometer at a place where the earth's horizontal magnetic field is 25 μT. Another short magnet of magnetic moment 1.6 A m2 is placed 20 cm east of the oscillating magnet. Find the new frequency of oscillation if the magnet has its north pole (a) towards north and (b) towards south.
