Advertisements
Advertisements
प्रश्न
A battery of e.m.f. 15 V and internal resistance 2 `Omega` is connected to tvvo resistors of 4 ohm and 6 ohm joined.
(i) In series,
(ii) In para 1 lel. Find in each case the electrica I energy spent per minute in 6 ohm resistor.
उत्तर
Given, emf= 15 V, internal resistance, r= 2 `Omega`
(i) Total resistance of given resistors in series, Rs = 4 + 6 = 10 `Omega`
Now, current through series combination on, Is = `"emf"/("R"_"s" + "r") = 15/(10 + 2) = 15/12` = 1.25 A
In series, the same current will pass through each resistor
.·. electrical energy spent per minute in the 6`Omega` resistor, Hs = I2 (R) t = (1.25)2 (6) (60) = 562.5 J
(ii) Total resistance of given resistors in parallel, RP = `(1/4 + 1/6) ^-1 = 2.4 Omega`
Current in parallel circuit, I = `15/(2.4 + 20) = 3.4 "A"`
In parallel, each resistor is connected across the same voltage, say V.
Then, V = e - Ir= 15 - (3.4 x 2) = 8.18 volt
:. electrical energy spent per minute in the 6Ω resistor, Hp = `"V"^2/"R" t = (8.18)^2/6 xx 60 `= 669.1 J
APPEARS IN
संबंधित प्रश्न
Differentiate between resistances in series and parallel.
Complete the following :-
(b)

A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24 Ω resistances, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Are the lights in your house wired in series?
Which of the following combinations have the same equivalent resistance between X and Y?
You have three resistors of values 2Ω, 3Ω and 5Ω. How will you join them so that the total resistance is less than 1Ω? Draw diagram and find the total resistance.
What is the equivalent resistance of 5 equal resistors, each of value 2`Omega` 1 when oonnected in (a) Series ( b) ParaIleI?
How does the resistance of a metallic wire depend on the length of wire?
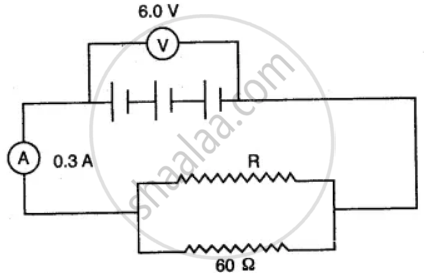
In the figure below, the ammeter A reads 0.3 A. Calculate:
(i) the total resistance of the circuit
(ii) the value of R
(iii) the current flowing through R.
The least resistance obtained by using 2 Ω, 4 Ω, 1 Ω and 100 Ω is:
