Question

A child starts running from rest along a circular track of radius r with constant tangential acceleration a. After time the feels that slipping of shoes on the ground has started. The coefficient of friction between shoes and the ground is [g = acceleration due to gravity].

पर्याय

• `(["a"^4"t"^4 + "a"^2"r"^2]^(1/2))/"gr"`

• `(["a"^4"t"^4 + "a"^2"r"^2])/"rg"`

• `(["a"^2"t"^2 + "a"^4"r"^4])/"rg"`

• `(["a"^4"t"^4 - "a"^2"r"^2]^(1/2))/"rg"`

Answer 1

`(["a"^4"t"^4 + "a"^2"r"^2]^(1/2))/"gr"`

Explanation:

When child moves in a circular track, he is acted upon by two force as shown below.

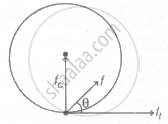
Here, f_c = f sin Sand f_t = f cos θ.
As, f_c is the centripetal force and f_t is the tangential force. So,

`"f"_"c" = "mv"^2/"r"`= f cos θ

and f_t = ma = f cos θ

∴ Resultant force, f_R = `sqrt(("f" sin theta)^2 + ("f" cos theta)^2)`

`= sqrt(("mv"^2/"r")^2 + ("ma")^2)`

Also, when the shoes starts slipping, the friction becomes equal to resultant force.

∴ f = f_R

`mu "mg" = sqrt(("mv"^2/"r")^2 + ("ma")^2)`

`=> mu^2 "m"^2 "g"^2 = ("m"^2"v"^4)/"r"^2 + "m"^2"a"^2`

`=> mu^2"g"^2 = (("at")^4 + "a"^2"r"^2)/"r"^2   ....(because "a" = "v"/"t")`

or `mu = (["a"^4"t"^4 + "a"^2"r"^2]^(1/2))/"gr"`