Advertisements
Advertisements
प्रश्न
- चित्र में अपवर्तनांक 1.68 के तंतु काँच से बनी किसी 'प्रकाश नलिका' (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है। नलिका का बाह्य आवरण 1.44 अपवर्तनांक के पदार्थ का बना है। नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते हैं, ज्ञात कीजिए।
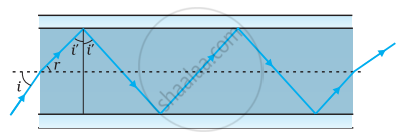
- यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा?
उत्तर
(a) वायु के सापेक्ष काँच का अपवर्तनांक, μ1 = 1.68
पाइप के बाहरी आवरण का अपवर्तनांक, μ2 = 1.44
आपतन कोण = i
अपवर्तन कोण = r
अंतरापृष्ठ पर आपतन कोण = i'
आंतरिक कोर - बाहरी कोर अंतरापृष्ठ का अपवर्तनांक (μ) निम्नानुसार दिया गया है:
`μ = μ_2/μ_1 = 1/(sin "i'")`
`sin "i'" = (μ_1)/(μ_2)`
= `1.44/1.68`
= 0.8571
∴ i' = 59°
क्रांतिक कोण के लिए, कुल आंतरिक परावर्तन केवल तभी होता है जब i > i', यानी, i > 59° हो।
अधिकतम परावर्तन कोण, rmax = 90° − i' = 90° − 59° = 31°
मान लीजिए, imax अधिकतम आपतन कोण है।
वायु-काँच अंतरापृष्ठ पर अपवर्तनांक, μ1 = 1.68
हमारे पास आपतन और परावर्तन के अधिकतम कोणों के लिए निम्न संबंध है:
`μ_1 = (sin "i"_"max")/sin "r"_"max"`
sin imax = μ1 sin rmax
= 1.68 sin 31°
= 1.68 × 0.5150
= 0.8652
∴ imax = sin−1 0.8652 ≈ 60°
इस प्रकार, 0 < i < 60° की सीमा में स्थित कोणों पर आपतित सभी किरणें पूर्ण आंतरिक परावर्तन से ग्रस्त होंगी।
(b) यदि पाइप का बाहरी आवरण मौजूद नहीं है, तो:
बाहरी पाइप का अपवर्तनांक, μ1 = वायु का अपवर्तनांक = 1
आपतन कोण i = 90° के लिए, हम वायु-पाइप इंटरफ़ेस पर स्नेल का नियम इस प्रकार लिख सकते हैं:
`sin "i"/sin "r" = μ_2` = 1.68
`sin "r" = (sin 90°)/1.68 = 1/1.68`
`"r" = sin^(-1) (0.5952)`
= 36.5°
∴ i' = 90° − 36.5° = 53.5°
चूँकि i' > r, सभी आपतित किरणें पूर्ण आंतरिक परावर्तन से गुजरेंगी।
