Question

A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The centre of mass of the new disc is α/R form the centre of the bigger disc. The value of α is ______.

पर्याय

• 1/4

• 1/3

• 1/2

• 1/6

Answer 1

A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The centre of mass of the new disc is α/R form the centre of the bigger disc. The value of α is 1/3.

Explanation:

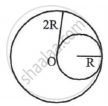
Let the mass per unit area be σ.

Then the mass of the complete disc = σ[π(2R)²] = 4πσR²

The removed disc's mass is equal to σ(πR²) = πσR². Consider the scenario above to be a full disc of radius 2R on top of which a disc of radius R with negative mass is superimposed. Make the origin O. Then, using the concept of the centre of mass, the previous illustration can be redrew as follows:

\[\begin{array}{cc}
\ce{4πσ\underset{\bullet}{R^2} <->[R][\bullet]}\\
\phantom{.......}\ce{O}\phantom{..}\ce{πσR^2}
\end{array}\]

`"X"_"c"."m"=((4pisigma"R"^2)xx0+(-pisigma"R"^2)"R")/(4pisigma-pisigma"R"^2)`

∴ `"x"_"c"."m".=(-pisigma"R"^2xx"R")/(3pisigma"R"^2)`

∴ `"x"_"c"."m".=-"R"/3`

⇒ α = `1/3`