Question

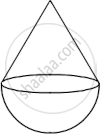
A company deals in casting and moulding of metal on orders received from its clients. In one such order, company is supposed to make 50 toys in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of hemisphere. If the radius of the base of the cone is 21 cm and height is 28 cm.

1. find the volume of 50 toys:
2. fine the ratio of the volume of hemisphere to the volume of cone.

Answer 1

a. Given, Radius of cone, r = 21 cm

Height of cone, h = 28 cm

Also, Radius of hemisphere, r = 21 cm

Volume of 50 toys = 50 × [Volume of sphere + Volume of cone]

= `50 xx (2/3 πr^3 + 1/3 πr^2h)`

= `50 xx 1/3(2 xx 22/7 xx (21)^3 + 22/7(21)^2 xx 28)`

= `50/3 xx 22/7 xx (21)^2 [2 xx 21 + 28]`

= `(50 xx 22 xx 21 xx 21 xx 70)/(7 xx 3)`

= 50 × 22 × 21 × 70

= 1617000 cm³

Hence, volume of 50 toys is 1617000 cm³

b. `"Volume of hemisphere"/"Volume of cone" = (2/3 πr^3)/(1/3 πr^2h)`

= `(2r)/h`

= `(2 xx 21)/28`

= `21/14 = 3/2`

Hence, the required ratio is 3 : 2.