Advertisements
Advertisements
प्रश्न
A device 'X' is connected to an ac source V = V0 sin ωt. The variation of voltage, current and power in one cycle is shown in the following graph:

(a) Identify the device 'X'.
(b) Which of the curves A, B and C represent the voltage , current and the power consumed in the circuit? Justify your answer.
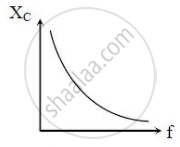
(c) How does its impedance vary with frequency of the ac source? Show graphically.
(d) Obtain an expression for the current in the circuit and its phase relation with ac voltage.
उत्तर
(a) The device 'X' is a pure capacitor.
(b) Curve A represents power P=VI, where the amplitude is equivalent to the multiplication of amplitudes of V and I curve. Curve B is the sine curve and represents voltage and curve C is a cosine curve representing the current.
The full cycle of the graph consists of two positive and two negative symmetrical areas. So the average power consumed in the circuit is zero.
(c) The AC impedance of a capacitor is known as Reactance and as we are dealing with capacitor circuits, more commonly called Capacitive Reactance. The graph shows variation of a capacitive reactance with frequency.
`z= x_c = 1/omega_c`
`x_c=1/(2pif_c)`
`v_c prop 1/f`
(d)
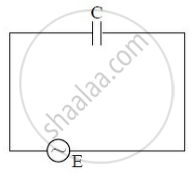
AC through capacitor:- Let us consider a capacitor with capacitance C be connected to an AC source with an emf having an instantaneous value
`E = E_0 sinomegat`..(i)
Due to this emf, a charge will be produced and it will charge the plates of a capacitor with a positive and negative charge. if potential difference across the plates of a capacitor is V then
`V=q/C " or" q=CV`
The instantaneous value of current in the circuit
`I = (dq)/dt=(d(CE))/(dt)` (∵ V = E)
`=d/(dt)(CE_0sinomegat)` `(because E = E_0sinomegat)`
`=CE_0cosomegat xx omega`
`=E_0/(1/omega_c)sin(omegat)` `[thereforecosomegat = sin(pi/2+omegat)]`
`I=E_0/(1/omega_c)sin(omegat+pi/2)`...............(ii)
`I` will be maximum when `sin(omegat+pi/2)=1` so that `I=I_0`
where peak value of current `I_0E_0/(1/omega_c)`
`I=Isin(omegat+pi/2)`..............(iii)
from (1) and (iii) it is clear current leads the voltage by a phase angle of `pi/2(a_0)`
संबंधित प्रश्न
An alternative voltage given by V = 140 sin 314t is connected across a pure resistor of 50 Ω. Find
- The frequency of the source.
- The rms current is through the resistor.
A 100 Ω resistor is connected to a 220 V, 50 Hz ac supply.
- What is the rms value of current in the circuit?
- What is the net power consumed over a full cycle?
A 100 Ω resistor is connected to a 220 V, 50 Hz ac supply.
What is the net power consumed over a full cycle?
Effective voltage Vrms is related to peak voltage Vo by ______.
If Vm and Im are peak voltage and current, impedance Z in an AC circuit is ______.
Study the circuits (a) and (b) shown in figure and answer the following questions.
 (a) |
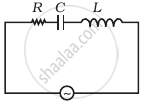 (b) |
- Under which conditions would the rms currents in the two circuits be the same?
- Can the rms current in circuit (b) be larger than that in (a)?
Can the instantaneous power output of an ac source ever be negative? Can the average power output be negative?
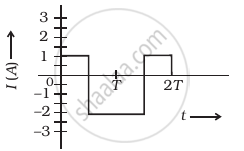
The alternating current in a circuit is described by the graph shown in figure. Show rms current in this graph.
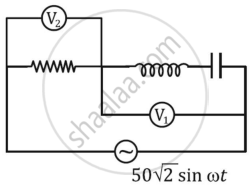
If the reading of the voltmeter V1 is 40 V, then the reading of voltmeter V2 is ______.