Advertisements
Advertisements
प्रश्न
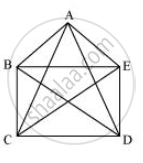
A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
उत्तर
It can be observed here that AC, AD, BD, BE, CE are the diagonals.
APPEARS IN
संबंधित प्रश्न
Construct traingle ABC, when : AC = 6 cm, ∠A = 60“ and ∠C = 45°. Measure AB and BC.
In the following figure, triangle ABC is equilateral and triangle PBC is isosceles. If PBA = 20°; find angle PBC.
In the following figure, triangle ABC is equilateral and triangle PBC is isosceles. If PBA = 20°; find angle BPC.
Using ruler and a pair compass only, construct a triangle PQR, given PQ = 5.5 cm, QR = 7.5 cm and RP = 6 cm. Draw the bisectors of the interior angles at P, Q and R. Do these bisectors meet at the same point ?
Name the following triangle in two different ways: (you may judge the nature of the angle by observation)
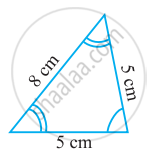
Try to construct triangles using match sticks. Some are shown here.
 |
 |
 |
Can you make a triangle with 3 matchsticks?
(Remember you have to use all the available matchsticks in each case) Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it.
Try to construct triangles using match sticks. Some are shown here.
 |
 |
 |
Can you make a triangle with 4 matchsticks?
(Remember you have to use all the available matchsticks in each case) Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it.
Try to construct triangles using match sticks. Some are shown here.
 |
 |
 |
Can you make a triangle with 5 matchsticks?
(Remember you have to use all the available matchsticks in each case) Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it.
Try to construct triangles using match sticks. Some are shown here.
 |
 |
 |
Can you make a triangle with 6 matchsticks?
(Remember you have to use all the available matchsticks in each case) Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it.
Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.
