Question

A dielectric slab of dielectric constant ‘K' and thickness ‘t' is inserted between plates of a parallel plate capacitor of plate separation d and plate area A. Obtain an expression for its capacitance.

Answer 1

The capacitance of a parallel plate capacitor of plate area A and plate separation d with vacuum between its plates is given by

`C_0 = (epsilon_0A)/d`

Suppose initially the charges on the capacitor plates are ±Q. Then the uniform electric field set up between the capacitor plates is

`E_0 = sigma/epsilon_0 = Q/(Aepsilon_0)`

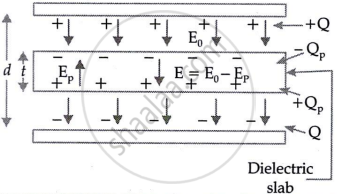
When a dielectric slab of thickness t < d is placed between the plates, the induced field is given by

`W_p = sigma_p/epsilon_0 = p/epsilon_0`    ...`[sigma_p = Q/A = P, "polarisation density"]`

The net field inside the dielectric is

`E = E_0 - E_p = E_0/k   ...[because E_0/(E_0 - E_p) = k]`

where k is the dielectric constant of the slab. Hence, the potential difference between the capacitor plates is

V = E₀(d − t) + Et

= `E_0(d - t) + E_0/kt   ...[because E_0/E = k]`

= `E_0(d - t + t/k)`

= `Q/(epsilon_0A)(d - t + t/k)`

The capacitance of the capacitor on introduction of dielectric slab becomes

`C = Q/V = (epsilon_0A)/(d - t + t/k)`