Advertisements
Advertisements
प्रश्न
A first order reaction takes 40 minutes for 30% decomposition. Calculate t1/2 for this reaction. (Given log 1.428 = 0.1548)
उत्तर
|
`A->P` |
||
| t=0 | a | 0 |
| t=t | (a-x) | x |
Now, it takes 40 min for 30% decomposition i.e. reactant left after 40 min is 70% of its initial concentration.
`So,(a-x)=70/100xxa=7/10xxa`
`k=2.303/tlog(a/(a-x)) => k=2.303/40 log a/(7/10)a=2.303/40log1.428`
`therefore k=0.00891 min `
`therefore t_(1/2)=0.693/k=0.693/0.008913=77.78 min`
APPEARS IN
संबंधित प्रश्न
For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
A first order reaction takes 30 minutes for 50% completion. Calculate the time required for 90% completion of this reaction.
(log 2 = 0.3010)
Calculate the half-life of a first order reaction from the rate constant given below:
200 s−1
Show that the time required for 99% completion is double of the time required for the completion of 90% reaction.
Half life (t1/2) and completion time (T) of the zero order reaction are- (K = 0.001 mol/litre/sec and a = 1 M.)
Observe the graph shown in figure and answer the following questions:
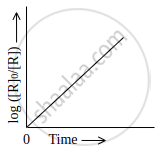
Write the relationship between k and t1/2 (half-life period)
Assertion (A): The half-life of a reaction is the time in which the concentration of the reactant is reduced to one-half of its initial concentration.
Reason (R): In first-order kinetics, when the concentration of reactant is doubled, its half-life is doubled.
Calculate the half-life of a first order reaction from the rate constant given below:
2 min−1
Calculate the half-life of a first order reaction from the rate constant given below:
4 year−1
A first order reaction takes 40 min for 30% decomposition. Calculate `"t"_(1/2)`.
