Advertisements
Advertisements
प्रश्न
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and `1/8` space of the cube remains unfilled. Number of marbles required is
पर्याय
142296
142396
142396
142596
उत्तर
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and `1/8` space of the cube remains unfilled. Number of marbles required is 142296.
Explanation:
since `1/8` th of the cube remains unfulfilled,
volume of the cube `= 22xx22xx22 "cm"^3`
space filled in the cube `= (7/8xx22xx22xx22) "cm"^3`
= (7×1331) cm3
Radius of each marble `= 0.5/2 "cm"`
`=5/20 "cm"`
`= 1/4 "cm"`
Volume of each marble `= 4/3 pir^3`
`= (4/3 xx 22/7xx1/4xx1/4xx1/4) "cm"^3`
`= (11/24 xx 7) "cm"^3`
Therefore, number of marbles required `= ((7xx1331xx24xx7)/11)`
= 142296
APPEARS IN
संबंधित प्रश्न
A spherical ball of radius 3cm is melted and recast into three spherical balls. The radii of the two of balls are 1.5cm and 2cm . Determine the diameter of the third ball?
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
12 spheres of the same size are made from melting a solid cylinder of 16 cm diameter and 2 cm height. The diameter of each sphere is
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
A well 28.8 m deep and of diameter 2 m is dug up. The soil dug out is spread all around the well to make a platform 1 m high considering the fact losse soil settled to a height in the ratio 6 : 5 find the width of the platform.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
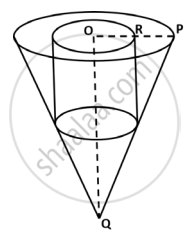
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
