Advertisements
Advertisements
प्रश्न
A man repays a loan of ₹ 65,000 by paying ₹ 400 in the first month and then increasing the payment by ₹ 300 every month. How long will it take for him to clear the loan?
उत्तर
Loan Amount = ₹ 65,000
Repayment through installments
400 + 700 + 1000 + 1300 + …
a = 400
d = 300
Sn = 65000
Sn = `"n"/2` (2a + (n – 1)d)
= 65000
`"n"/2` (2 × 400 + (n – 1)300) = 65000
n(800 + 300n – 300) = 130000
n(500 + 300n) = 130000
500n + 300n2 = 130000
300n2 + 500n = 130000
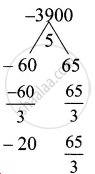
3n2 + 5n – 1300 = 0
(n – 20) (3n + 65) = 0
n = 20, n = `(-65)/3`
∴ n = 20
Number of terms should be (+ ve) and cannot be (– ve) or fractional number.
∴ He will take 20 months to clear the loans.
APPEARS IN
संबंधित प्रश्न
Find the sum of the following
102, 97, 92, … up to 27 terms.
How many consecutive odd integers beginning with 5 will sum to 480?
Find the sum of first 28 terms of an A.P. whose nth term is 4n – 3
The 104th term and 4th term of an A.P. are 125 and 0. Find the sum of first 35 terms
Find the sum of all odd positive integers less than 450
Find the sum of all natural numbers between 602 and 902 which are not divisible by 4.
A brick staircase has a total of 30 steps. The bottom step requires 100 bricks. Each successive step requires two bricks less than the previous step
How many bricks are required for the top most step?
A brick staircase has a total of 30 steps. The bottom step requires 100 bricks. Each successive step requires two bricks less than the previous step
How many bricks are required to build the stair case?
If S1, S2 , S3, …., Sm are the sums of n terms of m A.P.'s whose first terms are 1, 2, 3, ……, m and whose common differences are 1, 3, 5, …., (2m – 1) respectively, then show that S1 + S2 + S3 + ... + Sm = `1/2` mn(mn + 1)
In an A.P., the first term is 1 and the common difference is 4. How many terms of the A.P. must be taken for their sum to be equal to 120?
