Advertisements
Advertisements
प्रश्न
A person standing at a junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 seek to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find the equation of the path that he should follow.
उत्तर
Two straight paths will intersect at one point.
Solving this equation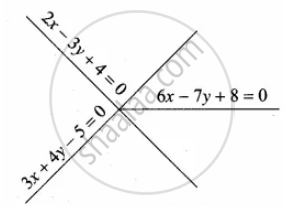
2x – 3y + 4 = 0
2x – 3y = – 4 ...(1)
3x + 4y = 5 ...(2)
(1) × 4 ⇒ 8x – 12y = – 16 ...(3)
(2) × 3 ⇒ 9x + 12y = 15 ...(4)
(3) + (4) ⇒ 17x = – 1
x = `(-1)/17`
Substitute the value of x = `(-1)/17` in (2)
`3(- 1/17) + 4y` = 5
⇒ `-3/17 + 4y` = 5
4y = `5 + 3/17`
= `(85 + 3)/17`
4y = `88/17`
⇒ y = `88/(17 xx 4)`
= `22/17`
The point of intersection is `(-1/17, 22/17)`
Any equation perpendicular to 6x – 7y + 8 = 0 is 7x + 6y + k = 0
It passes through `(-1/17, 22/17)`
`7(-1/17) + 6(22/17) + "k"` = 0
Multiply by 17
– 7 + 6(22) + 17k = 0
– 7 + 132 + 17k = 0
17k = – 125
⇒ k = `- 125/17`
The equation of a line is `7x + 6y - 125/17` = 0
119x + 102y – 125 = 0
∴ Equation of the path is 119x + 102y – 125 = 0
APPEARS IN
संबंधित प्रश्न
Find the slope of the following straight line
5y – 3 = 0
Find the slope of the following straight line
`7x - 3/17` = 0
Find the slope of the line which is perpendicular to the line x = – 11
Find the equation of a line passing through (6, −2) and perpendicular to the line joining the points (6, 7) and (2, −3)
Find the equation of the perpendicular bisector of the line joining the points A(− 4, 2) and B(6, − 4)
Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x – 2y – 4 = 0 to the point of intersection of 7x – 3y = – 12 and 2y = x + 3
Find the equation of a straight line through the point of intersection of the lines 8x + 3y = 18, 4x + 5y = 9 and bisecting the line segment joining the points (5, −4) and (−7, 6)
The straight line given by the equation x = 11 is
The equation of a line passing through the origin and perpendicular to the line 7x − 3y + 4 = 0 is
Consider four straight lines
(i) l1; 3y = 4x + 5
(ii) l2; 4y = 3x – 1
(iii) l3; 4y + 3x = 7
(iv) l4; 4x + 3y = 2
Which of the following statement is true?
