Advertisements
Advertisements
प्रश्न
A playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π = 22/7).
उत्तर
It is given that the playground is in the shape of a rectangle with two semicircles on its smaller sides.
Length of the rectangular portion is 36 m and its width is 24 . 5 m as shown in the figure below.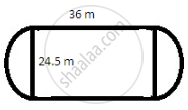
Thus, the area of the playground will be the sum of the area of a rectangle and the areas of the two semicircles with equal diameter 24 . 5 m.
Now, area of rectangle with length 36m and width 24 . 5m:
Area of rectangle = length x width
= 36m x 24 . 5 m
\[ = 882 m^2 \]
Radius of the semicircle = r =\[ \frac{\text{ diameter }}{2} = \frac{24 . 5}{2} = 12 . 25m\]
∴ Area of the semicircle \[ = \frac{1}{2} \pi r^2 \]
\[ = \frac{1}{2} \times \frac{22}{7} \times (12 . 25 )^2 \]
\[ = 235 . 8 m^2 \]
∴ Area of the complete playground = area of the rectangular ground + 2 x area of a semicircle
\[ = 882 + 2 \times 235 . 8\]
\[ = 1353 . 6 m^2\]
APPEARS IN
संबंधित प्रश्न
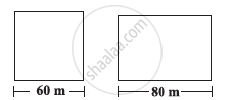
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food − piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.

A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Fig. 20.23. If AB = 60 m and BC = 28 m, find the area of the plot.
A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 m have been cut. Find the area of the remaining part.
The inside perimeter of a running track (shown in Fig. 20.24) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.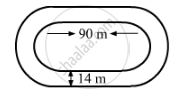
Find the area of Fig. 20.25, in square cm, correct to one place of decimal. (Take π = 22/7)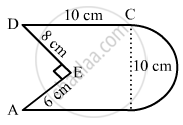
The length and the breadth of a rectangular plot are 135 m and 65 m. Find, its perimeter and the cost of fencing it at the rate of ₹60 per m.
The perimeter of a rectangle becomes ______ times its original perimeter, if its length and breadth are doubled.
The length of an aluminium strip is 40 cm. If the lengths in cm are measured in natural numbers, write the measurement of all the possible rectangular frames which can be made out of it. (For example, a rectangular frame with 15 cm length and 5 cm breadth can be made from this strip.)
