Advertisements
Advertisements
प्रश्न
A rectangular field is of dimension 20 m × 15 m. Two paths run parallel to the sides of the rectangle through the centre of the field. The width of the longer path is 2 m and that of the shorter path is 1 m. Find (i) the area of the paths (ii) the area of the remaining portion of the field (iii) the cost of constructing the roads at the rate of ₹ 10 per sq.m
Advertisements
उत्तर
Length of the rectangular field L = 20 m
Breadth B = 15 m
Area = L × B
= 20 × 15 m2
Area of outer rectangle = 300 m2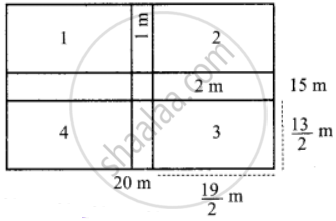 
Area of inner small rectangle = `19/2 xx 13/2` = 61.75 cm2
(i) Area of the path = Area of the outer rectangle – Area of 4 inner small rectangles
= 300 – 4(61.75)
= 300 – 247
= 53 m2
Area of the paths = 53 m2
(ii) Area of the remaining portion of the field
= Area of the outer rectangle – Area of the paths
= 300 – 53 m2
= 247 m2
Area of the remaining portion = 247 m2
(iii) Cost of constructing 1 m2 road = ₹ 10
∴ Cost of constructing 53 m2 road = ₹ 10 × 53 = ₹ 530
∴ Cost of constructing road = ₹ 530
APPEARS IN
संबंधित प्रश्न
There is a circular lawn of radius 28 m. A path of 7 m width is laid around the lawn. What will be the area of the path?
A circular carpet whose radius is 106 cm is laid on a circular hall of radius 120 cm. Find the area of the hall uncovered by the carpet
A school ground is in the shape of a circle with radius 103 m. Four tracks each of 3 m wide has to be constructed inside the ground for the purpose of track events. Find the cost of constructing the track at the rate of ₹ 50 per sq.m
The formula to find the width of the circular path is
Four circles are drawn side by side in a line and enclosed by a rectangle as shown below. If the radius of each of the circles is 3 cm, then calculate:
(i) The area of the rectangle.
(ii) The area of each circle.
(iii) The shaded area inside the rectangle.
A cow is tethered with a rope of length 35 m at the centre of the rectangular field of length 76 m and breadth 60 m. Find the area of the land that the cow cannot graze?
A path 5 m wide runs along the inside of the rectangular field. The length of the rectangular field is three times the breadth of the field. If the area of the path is 500 m2 then find the length and breadth of the field
A circular path has to be constructed around a circular ground. If the areas of the outer and inner circles are 1386 m2 and 616 m2 respectively, find the width and area of the path
A goat is tethered with a rope of length 45 m at the centre of the circular grassland whose radius is 52 m. Find the area of the grassland that the goat cannot graze
A strip of 4 cm wide is cut and removed from all the sides of the rectangular cardboard with dimensions 30 cm × 20 cm. Find the area of the removed portion and area of the remaining cardboard
