Advertisements
Advertisements
प्रश्न
A side of an equilateral triangle is 20 cm long. A second equilateral triangle is inscribed in it by joining the midpoints of the sides of the first triangle. The process is continued as shown in the accompanying diagram. Find the perimeter of the sixth inscribed equilateral triangle.
उत्तर
The side of the first equilateral ΔABC = 20 cm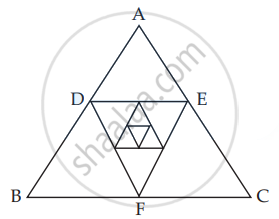
By joining the midpoints of the sides of this triangle
We get the second equilateral triangle which each side
= `20/2`
= 10 cm
[∵ The line joining the mid-points of two sides of a triangle is `1/2` and parallel to third side of the triangle]
Similarly each side of the third equilateral triangle = `10/2` = 5cm
∴ Perimeter of first triangle = 20 × 3 = 60 cm
Perimeter of the second triangle = 10 × 3 = 30 cm
And the perimeter of the third triangle = 5 × 3 = 15 cm
Therefore, the series will be 60, 30, 15, …
Which is G.P. in which a = 60
And r = `30/60 = 1/2`
Now, we have to find the perimeter of the sixth inscribed equilateral triangle
∴ a6 = ar6–1
= `60 xx (1/2)^5`
= `60 xx 1/32`
= `15/8` cm
Hence, the required perimeter = `15/8` cm.
APPEARS IN
संबंधित प्रश्न
The 10th common term between the series 3 + 7 + 11 + ... and 1 + 6 + 11 + ... is ______.
We know the sum of the interior angles of a triangle is 180°. Show that the sums of the interior angles of polygons with 3, 4, 5, 6, ... sides form an arithmetic progression. Find the sum of the interior angles for a 21 sided polygon.
In a potato race 20 potatoes are placed in a line at intervals of 4 metres with the first potato 24 metres from the starting point. A contestant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
In a cricket tournament 16 school teams participated. A sum of Rs 8000 is to be awarded among themselves as prize money. If the last-placed team is awarded Rs 275 in prize money and the award increases by the same amount for successive finishing places, how much amount will the first-place team receive?
