Question

A simple pendulum of length I has a bob of mass m. It executes SHM of small amplitude A. The maximum tension in the string is (g = acceleration due to gravity)

पर्याय

• mg

• `"mg"("A"^2/"l"^2 + 1)`

• 2 mg

• `"mg"("A"/"l" + 1)`

Answer 1

`"mg"("A"^2/"l"^2 + 1)`

Explanation:

Consider the figure shown below

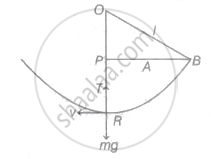
The string possess maximum tension when bob is at mean position of oscillation i.e., at position R.

From geometry, OP = `sqrt("l"^2 - "A"^2)`

Also, RP = OR - OP = l - `sqrt("l"^2 - "A"^2)`

The whole kinetic energy of bob at position R is converted into its potential energy at position B.

`therefore 1/2 "mv"^2 = "mg"("l" - sqrt("l"^2 - "A"^2))`

`"v"^2 = "2g"("l" - sqrt("l"^2 - "A"^2))`

Balancing forces at R,

T - mg = `"mv"^2/"l" = (2"mg" ("l" - sqrt("l"^2 - "A"^2)))/"l"`

∴ T = mg + 2mg `(1 - sqrt(1 - "A"^2/"l"^2))`

Using approximation, `sqrt(1 - x^2) = 1 - x^2/2` for x << 1, we get

T = mg = 2mg `[1 - (1 - "A"^2/(2"l"^2))]`

= mg + mg`("A"/"l")^2`

= mg `[1 + ("A"/"l")^2]`