Advertisements
Advertisements
प्रश्न
A solid sphere moves at a terminal velocity of 20 m s−1 in air at a place where g = 9.8 m s−2. The sphere is taken in a gravity-free hall having air at the same pressure and pushed down at a speed of 20 m s−1.
(a) Its initial acceleration will be 9.8 m s−2 downward.
(b) It initial acceleration will be 9.8 m s−2 upward.
(c) The magnitude of acceleration will decrease as the time passes.
(d) It will eventually stop
उत्तर
(b) There is no gravitational force acting downwards. However, when the starting velocity is 20 m/s, the viscous force, which is directly proportional to velocity, becomes maximum and tends to accelerate the ball upwards.
\[\text{ When the ball falls under gravity, }\]
\[\text{ neglecting the density of air: } \]
\[\text{ Mass of the sphere = m }\]
\[\text{ Radius = r }\]
\[\text{ Viscous drag coeff . }= \eta\]
\[\text{Terminal velocity is given by}: \]
\[\text{ mg }= 6\pi\eta r v_T \]
\[ \Rightarrow \frac{6\pi\eta r v_T}{m} = g . . . (1)\]
\[\text{ Now, at terminal velocity, the acceleration of the ball due to the viscous force is given by: } \]
\[a = \frac{6\pi\eta r v_T}{m}\]
\[\text{ Comparing equations (1) and (2), we find that : } \]
\[ \text{ a = g }\]
Thus, we see that the initial acceleration of the ball will be 9.8 ms - 2 .
(c) The velocity of the ball will decrease with time because of the upward viscous drag. As the force of viscosity is directly proportional to the velocity of the ball, the acceleration due to the viscous force will also decrease.
(d) When all the kinetic energy of the ball is radiated as heat due to the viscous force, the ball comes to rest.
APPEARS IN
संबंधित प्रश्न
A piece of wood is taken deep inside a long column of water and released. It will move up
A solid sphere falls with a terminal velocity of 20 m s−1 in air. If it is allowed to fall in vacuum,
A metal sphere of radius 'R' and density 'ρ1' is dropped in a liquid of density 'σ' moves with terminal velocity 'v'. Another metal sphere of same radius and density 'ρ2' is dropped in the same liquid, its terminal velocity will be ______.
Two spheres of equal masses but radii r1 and r2 are allowed to fall in a liquid of infinite column. The ratio of their terminal velocities are ____________.
A drop of radius 1.5 x 10-5 and density 2 x 103 kg/m3 falls through air. The viscosity of air is 1.8 x 10-5 N s/m2. Neglecting buoyancy due to air, the terminal speed of the drop is ____________.
A drop of radius 4 x 10-5 m and density 2.5 x 103 kg/m3 falls through air. The viscosity of air is 1.96 x 10-5 N s/m2 . Neglecting buoyancy due to air, the terminal speed of the drop is ____________.
Two small spherical metal balls, having equal masses, are made from materials of densities `rho_1` and`rho_2 (rho_1 = 8rho_2)` and have radii of 1 mm and 2 mm, respectively, they are made to fall vertically (from rest) in a viscous medium whose coefficient of viscosity equals `eta` and whose density is `0.1rho_2` The ratio of their terminal velocities would be, ____________.
The radii of the two spheres P and Q of same material falling in the viscous liquid are in the ratio 3 : 2, their terminal velocities (P to Q) are in the ratio ______.
A small spherical solid ball is dropped from a great height in a viscous liquid. Its journey in the liquid is best described in the diagram given below by the ____________.
Two rain drops falling through air have radii in the ratio 1 : 2. They will have terminal velocity in the ratio ______.
A small spherical ball of radius 0.1 mm and density 104 kg m-3 falls freely under gravity through a distance of h before entering a tank of water. If, after entering the water the velocity of the ball does not change and it continues to fall with the same constant velocity inside the water, then the value of h will be ______ m.
(Given g = 10 ms-2, the viscosity of water = 1.0 × 10-5 N-sm-2).
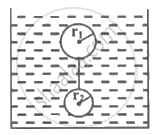
Two solid spherical balls of radius r1 and r2 (r2 < r1), of density σ are tied up with a long string and released in a viscous liquid column of lesser density ρ and coefficient of viscosity η, with the string just taut as shown. The terminal velocity of spheres is ______.
A spherical solid ball of volume V is made up of a material of density ρ1. It is falling through the liquid of density ρ2(ρ2 < ρ1). Assume that, the liquid applies a viscous force on the ball that is proportional to the square of the speed vt, i.e., `["F"_"viscous" = "KV"_"t"^2]`, then the terminal speed of the ball is ______.
(g = acceleration due to gravity)
Two equal drops of water are falling through air with a steady velocity v. If the drops coalesce, the new velocity will be ______.
