Question

A spherical solid ball of volume V is made of a material of density ρ₁. It is falling through a liquid of density ρ₂ (ρ₂ < ρ₁). Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed v, i.e., `"F"_"viscous"`= -kv² (k > 0). The terminal speed of the ball is ______.

पर्याय

• `sqrt(("Vg"(rho_1-rho_2))/"k")`

• `("Vg"rho_1)/"k"`

• `sqrt(("Vg"rho_1)/"k")`

• `("Vg"(rho_1-rho_2))/"k"`

Answer 1

A spherical solid ball of volume V is made of a material of density ρ₁. It is falling through a liquid of density ρ₂ (ρ₂ < ρ₁). Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed v, i.e., `"F"_"viscous"`= -kv² (k > 0). The terminal speed of the ball is `underlinebb(sqrt(("Vg"(rho_1-rho_2))/"k"))`.

Explanation:

The condition for terminal speed (v_t) is Weight = Buoyant force + Viscous force

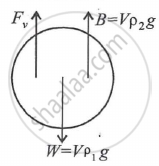
∴ Vρ₁g = Vρ₂g + k`"v"_"t"^2`

∴ v_t = `sqrt(("Vg"(rho_1-rho_2))/"k")`