Question

A stone of mass 1 kg is tied to a string 2m long and it's rotated at constant speed of 40 ms- 1 in a vertical circle. The ratio of the tension at the top and the bottom is ______.
[Take g = 10 ms^-2]

पर्याय

• `81/79`

• `79/81`

• `19/12`

• `12/19`

Answer 1

A stone of mass 1 kg is tied to a string 2m long and it's rotated at constant speed of 40 ms- 1 in a vertical circle. The ratio of the tension at the top and the bottom is `underline(79/81)`.

Explanation:

A free body diagram (FBD) shows a stone travelling in a vertical circular path, with tension forces at points A and Bas, represented by T_A and T_B, respectively, as shown in the graphic below.

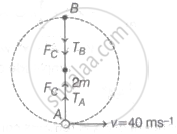
Given, mass of stone (m) = 1 kg,
length of the string (R) = 2 m and
rotating linear speed (v) = 40ms^-1 

As, we know that the tension at position A

`"T"_"A" = "mv"^2/"R" + "mg"    ...(therefore "F"_"c" = "mv"^2/"R")`

`=> "T"_"A" = (1 xx (40)^2)/2 + 1 xx 10`

= 810 N

Similarly, tension at position B,

`"T"_"B" = "mv"^2/"R" - "mg"`

`= (1 xx (40)^2)/2 - 1 xx 10`

= 790 N

So, the ratio of T_B and T_A i.e.,

`"T"_"B"/"T"_"A" = 790/810 = 79/81`

Hence, the ratio of tension at position B and tension at position A is 79 : 81.