Question

A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is ______.

पर्याय

• 3

• 2

• 1

• 5

Answer 1

A stone tide to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in its velocity, as it reaches a position where the string is horizontal, is `sqrt(x("u"^2 - "gL")`. The value of x is 2.

Explanation:

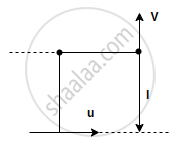
`Deltavec"V"=|vec"V"-vec"u"|=sqrt("V"^2+"u"^2)`        `[∵ vec"V" ⊥ vec"u"]`

Now, `"K"_1+"P"_1="K"_2+"P"_2`

⇒ `1/2"mu"^2+0=1/2"mV"^2+"mg l"`

⇒ V² = u² - 2g l

So, `Delta"V" = sqrt("V"^2+"u"^2)`

= `sqrt("u"^2-2"gl"+"u"^2)`

= `sqrt(2("u"^2-"gl"))`