Question

Use Graph paper for this question.

A survey regarding height (in cm) of 60 boys belonging to Class 10 of a school was conducted. The following data was recorded:

Height in cm	135-140	140-145	145-150	150-155	155-160	160-165	165-170
No. of boys	4	8	20	14	7	6	1

Taking 2 cm = height of 10 cm along one axis and 2 cm = 10 boys along the other axis draw an ogive of the above distribution. Use the graph to estimate the following:

1) the median

2) lower Quartile

3) if above 158 cm is considered as the tall boys of the class. Find the number of boys in the class who are tall.

Answer 1

The cumulative frequency table of the given distribution table is as follows:

Height in cm	No. of boys (f)	Cumulative frequency
135-140	4	4
140-145	8	12
145-150	20	32
150-155	14	46
155-160	7	53
160-165	6	59
165-170	1	60

Plot the points (140, 4), (145, 12), (150, 32), (155, 46), (160, 53), (165, 59) and
(170, 60) on a graph paper and join them to get an ogive.

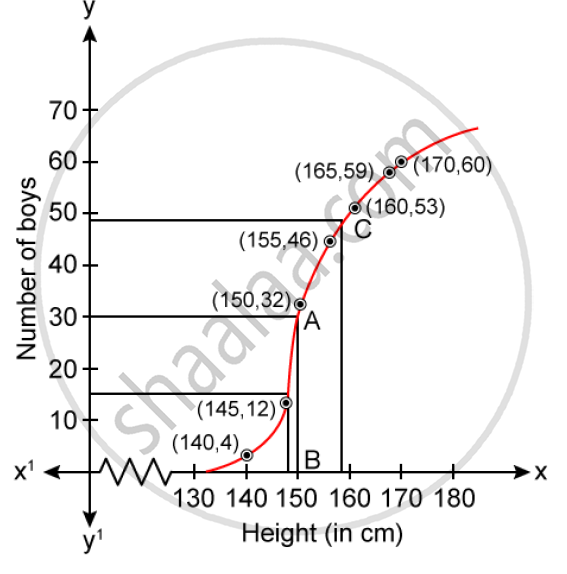
Number of boys = N = 60

1) Media = `(N/2)`th term = `(60/2)th` term  = 30 th term

Through mark 30 on the Y-axis, draw a horizontal line which meets the curve at point A.

Through point A, on the curve draw a vertical line which meets the X-axis at point B.

The value of point B on the X-axis is the median, which is 152

2) Lower quartile (Q₁) = `(N/4)th term = (60/4) th  term = 15 th term = 148`

3) Through mark of 158 on X-axis, draw a verticle line which meets the graph at point C.

Then through point C, draw a horizontal line which meets the Y-axis at the mark of 48.

Thus the number of boys in the class who are tall =  60 - 48 = 12