Advertisements
Advertisements
प्रश्न
आकृती मध्ये, बिंदू B हा स्पर्शबिंदू आणि बिंदू O वर्तुळकेंद्र आहे. रेख OE ⊥ रेषा AD, AB = 12, AC = 8, तर (1) AD (2) DC आणि (3) DE काढा.
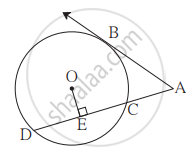
उत्तर
(1) रेषा AB ही वर्तुळाची B बिंदूत स्पर्श करणारी स्पर्शिका आहे आणि रेख AD ही छेदिका आहे. .......[पक्ष]
∴ AC × AD = AB2 ......[स्पर्शिका-छेदिका रेषाखंडांचे प्रमेय]
∴ 8 × AD = 122
∴ 8 × AD = 144
∴ AD = `144/8`
∴ AD = 18 एकक
(2) AD = AC + DC .....[A-C-D]
∴ 18 = 8 + DC
∴ DC = 18 - 8
∴ DC = 10 एकक
(3) रेख OE ⊥ रेख AD ....[पक्ष]
म्हणजेच, रेख OE ⊥ रेख CD .......[A - C - D]
∴ DE = `1/2` DC .......[वर्तुळकेंद्रापासून जीवेवर टाकलेला लंब जीवेस दुभागतो.]
= `1/2 xx 10`
∴ DE = 5 एकक
APPEARS IN
संबंधित प्रश्न
आकृती मध्ये, बिंदू Q हा स्पर्शबिंदू आहे. जर PQ = 12, PR = 8, तर PS = किती? RS = किती?
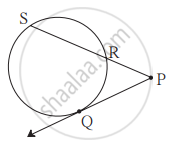
खालील आकृतीत बिंदू P हा स्पर्शबिंदू आहे.
m(कंस PR) = 140, ∠POR = 36° तर m(कंस PQ) = किती?
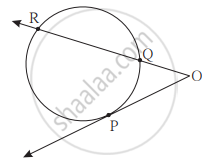
खालील आकृतीत बिंदू P हा स्पर्शबिंदू आहे.
OP = 7.2, OQ = 3.2, OR = किती? QR = किती?

खालील आकृतीत बिंदू P हा स्पर्शबिंदू आहे.
OP = 7.2, OR = 16.2, तर QR = किती?


वरील आकृतीमध्ये, ∠ABC हा कंस ABC मधील आंतरलिखित कोन आहे. जर ∠ABC = 60°, तर m∠AOC काढा.
उकल:
∠ABC = `1/2` m(कंस AXC) ...`square`
60° = `1/2` m(कंस AXC)
`square` = m(कंस AXC)
परंतु m∠ AOC = m(कंस `square`) ...(केंद्रीय कोनाचा गुणधर्म)
∴ m ∠AOC = `square`
