Question

AB and CD are two equal chords of a circle with centre O which intersect each other at right
angle at point P. If  OM⊥ AB and ON ⊥ CD; show that OMPN is a square.

Answer 1

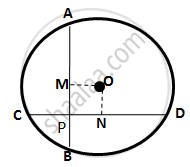
Clearly, all the angles of OMPN are 90°
OM⊥ AB and ON ⊥CD
∴ `BM =1/2 = AB=1/2  CD = CN`  ………….. (i)
(Perpendicular drawn from the centre of a circle to a chord bisects it)
As the two equal chords AB and CD intersect at point P inside
The circle,

∴ AP = DP  and CP = BP         ……………. (ii)
Now, CN - CP =  BM - BP (by (i) and (ii))
 ⇒ PN MP
∴ Quadrilateral OMPN is a square