Advertisements
Advertisements
प्रश्न
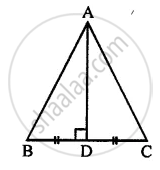
ABC is an equilateral triangle, AD and BE are perpendiculars to BC and AC respectively. Prove that:
(i) AD = BE
(ii) BD = CE
उत्तर
In Δ ABC,
AB = BC = CA,
AD ⊥ BC, BE ⊥ AC.
Proof: In Δ ADC and Δ BEC
∠ADC = ∠BEC ...........(each 90°)
∠ACD = ∠BCE ..............(common)
and AC = BC ............(sides of an equilateral triangle)
∴ Δ ADC ≅ Δ BEC ...........(A.A.S. Axiom)
Hence (i) AD = BE ...........(c.p.c.t.)
and (ii) BD = CE ...........(c.p.c.t.)
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, prove that: BD = BC.
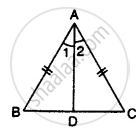
In the given figure ;
∠1 = ∠2 and AB = AC.
Prove that:
(i) ∠B = ∠C
(ii) BD = DC
(iii) AD is perpendicular to BC.
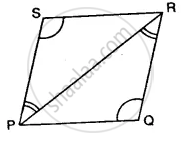
In the given figure prove that:
(i) PQ = RS
(ii) PS = QR
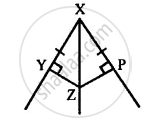
(i) ∆ XYZ ≅ ∆ XPZ
(ii) YZ = PZ
(iii) ∠YXZ = ∠PXZ
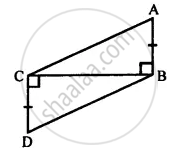
In the given figure, prove that:
(i) ∆ ABC ≅ ∆ DCB
(ii) AC = DB
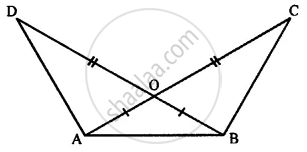
In the given figure, prove that:
(i) ∆ AOD ≅ ∆ BOC
(ii) AD = BC
(iii) ∠ADB = ∠ACB
(iv) ∆ ADB ≅ ∆ BCA
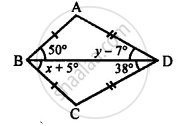
Use the information given in the following figure to prove triangles ABD and CBD are congruent. Also, find the values of x and y.
The given figure shows a triangle ABC in which AD is perpendicular to side BC and BD = CD. Prove that:
(i) ∆ ABD ≅ ∆ ACD
(ii) AB = AC
(iii) ∠B = ∠C