Advertisements
Advertisements
प्रश्न
ΔABC में, रेख AD ⊥ भुजा BC, रेख BE ⊥ भुजा AC, रेख CF ⊥ भुजा AB। बिंदु ‘O’ लंबपाद हो तो सिद्ध कीजिए कि, बिंदु ‘O’ ΔDEF का अंतःकेंद्र है।
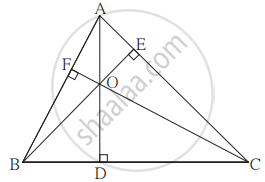
उत्तर

रेख EF, रेख DF और रेख DE खींचो |
रेख AD ⊥ भुजा BC,
रेख BE ⊥ भुजा AC,
रेख CF ⊥ भुजा AB ...................(दत्त) ..........(1)
∴ ∠BFC = ∠BEC = 90° ............[(1) से]
रेखा BC पर स्थित दो भिन्न बिंदु B और C उसी रेखा के एक ही ओर स्थित दो भिन्न बिंदु F और E पर सर्वांगसम कोण बनाता है |
∴ बिंदु B, F, E और C एक ही वृत्त पर हैं |
∴ ∠FEB ≅ ∠FCB ............(एक ही वृत्तचाप के अंतर्लिखित कोण)
∠OEC = ∠ODC = 90° ............[(1) से] ..........(2)
∴ ∠OEC + ∠ODC = 90° + 90° = 180°
∴ `square`OEDC चक्रीय चतुर्भुज है | ........(चक्रीय चतुर्भुज के प्रमेय का विलोम)
∴ ∠OED ≅ ∠OCD ................(एक ही वृत्त चाप के अंतर्लिखित कोण)
∴ ∠OED ≅ ∠FCB ..............(F-O-C, B-D-C) .............(3)
∴ ∠FEB ≅ ∠OED ...............[(2) और (3) से]
∴ ∠FEO ≅ ∠OED .........(B-O-E)
∴ रेख EO, ∠FED को समद्विभाजित करती है |
इसी प्रकार, हम सिद्ध कर सकते है कि, रेख DO ∠FDE को समद्विभाजित करती है तथा रेख FO, ∠EFD को समद्विभाजित करती है |
∴ बिंदु O ΔDEF के कोणों के समद्विभाजकों का प्रतिच्छेदन बिंदु है |
∴ बिंदु 'O' ΔDEF का अंतः केंद्र है |
उपरोक्त प्रश्न को समझने के लिए संकेत :
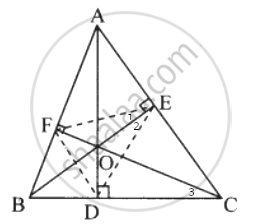
बिंदु F, E, C और B एक ही वृत्त पर हैं | यह सिद्ध करने पर, हमें प्राप्त होता है कि,
∠1 = ∠3 ..........(एक ही वृत्त चाप के अंतर्लिखित कोण)
तो, `square`OECD चक्रीय चतुर्भुज हैं यह सिद्ध करने पर,
हमें प्राप्त होता है कि, ∠2 = ∠3 ..................(एक ही वृत्त चाप के अंतर्लिखित कोण)
∴ ∠1 = ∠2
∴ रेख OE, ∠FED को समद्विभाजित करती है |
इसी प्रकार, हम सिद्ध कर सकते है कि, रेख DO, ∠FDE को समद्विभाजित करती है |
तथा रेख FO, ∠EFD को समद्विभाजित करती है |
∴ बिंदु O, अंतः केंद्र है |
APPEARS IN
संबंधित प्रश्न
सिद्ध कीजिए कि कोई भी आयत चक्रीय चतुर्भुज होता है।
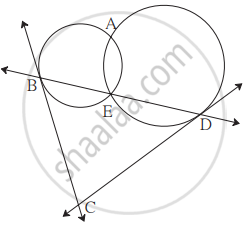
दो वृत्त परस्पर बिंदु A तथा बिंदु E पर प्रतिच्छेदित करते हैं। बिंदु E से खींची गई सामान्य छेदन रेखा वृत्तों को बिंदु B तथा बिंदु D पर प्रतिच्छेदित करती है। बिंदु B तथा बिंदु D से खींची गई स्पर्श रेखाएँ परस्पर बिंदु C पर प्रतिच्छेदित करती हैं। सिद्ध कीजिए कि, `square`ABCD एक चक्रीय चतुर्भुज है।