Question

ABCD is a rectangle formed by the points A (−1,−1), B (−1, 6), C (3, 6) and D (3, −1). P, Q, R and S are midpoints of sides AB, BC, CD and DA respectively. Show that diagonals of the quadrilateral PQRS bisect each other.

Answer 1

Given ABCD is a rectangle and P, Q, R, and S are midpoints of sides AB, BC, CD, and DA.

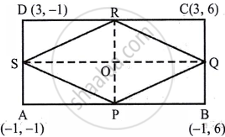
coordinates of P = `((-1 -1)/2, (-1 + 6)/2)`

= `(-1, 5/2)`

coordinates of Q = `((-1 + 3)/2, (6 + 6)/2)`

= (1, 6)

coordinates of R = `((3 + 3)/2, (6 - 1)/2)`

= `(3, 5/2)`

coordinates of S = `((3 - 1)/2, (-1 - 1)/2)`

= (1, −1)

Now, we shall find the midpoints of PR & SQ.

Midpoints of P & R, which is point O,

`x = (-1 + 3)/2 = 1`

`y = (5/2 + 5/2)/(2) = 5/2`

⇒ O(x, y) = `(1, 5/2)`

Similarly, the midpoint of S and Q

⇒ `x = (1 + 1)/2 = 1`

`y = (6 - 1)/2 = 5/2`

⇒ O(x, y) = `(1, 5/2)`

Since the midpoints of PR & QS both have the same coordinate `(1, 5/2)`. Hence, diagonals PR and SQ bisect to each other.

Hence Proved.