Advertisements
Advertisements
प्रश्न
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically
उत्तर
Let the present age of Aftab be x.
And, present age of his daughter = y
Seven years ago,
Age of Aftab = x − 7
Age of his daughter = y − 7
According to the question,
(x - 7) = 7(y - 7)
x - 7 = 7y - 49
x - 7y = - 42 ... (1)
Three years hence,
Age of Aftab = x + 3
Age of his daughter = y + 3
According to the question,
(x + 3) = 3(y + 3)
(x+3) = 3y+9
x - 3y = 6 ..... (2)
Therefore, the algebraic representation is
x - 7y = -42
x - 3y = 6
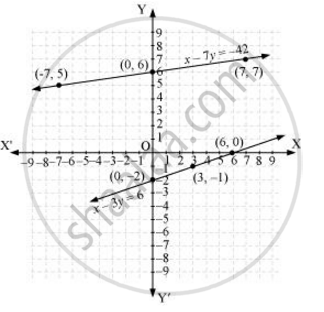
For x -7y = -42
x = -42 + 7y
The solution table is
|
x |
− 7 |
0 |
7 |
|
y |
5 |
6 |
7 |
For x-3y=6
Let the present age of Aftab be x.
And, present age of his daughter = y
Seven years ago,
Age of Aftab = x − 7
Age of his daughter = y − 7
According to the question,
(x - 7) = 7(y - 7)
x - 7 = 7y - 49
x - 7y = - 42 ... (1)
Three years hence,
Age of Aftab = x + 3
Age of his daughter = y + 3
According to the question,
(x + 3) = 3(y + 3)
(x+3) = 3y+9
x - 3y = 6 ..... (2)
Therefore, the algebraic representation is
x - 7y = -42
x - 3y = 6
For x -7y = -42
x = -42 + 7y
The solution table is
|
x |
− 7 |
0 |
7 |
|
y |
5 |
6 |
7 |
For x - 3y = 6
x = 6 + 3y
The solution table is
|
x |
6 |
3 |
0 |
|
y |
0 |
− 1 |
− 2 |
The graphical representation is as follows.
APPEARS IN
संबंधित प्रश्न
Find the value of k for which each of the following system of equations has infinitely many solutions :
x + (k + 1)y =4
(k + 1)x + 9y - (5k + 2)
Find the value of k for which each of the following system of equations has infinitely many solutions :
2x + (k - 2)y = k
6x + (2k - 1)y - (2k + 5)
Find the value of k for which each of the following system of equations have no solution
x + 2y = 0
2x + ky = 5
Solve for x and y:
217x + 131y = 913, 131x + 217y = 827
Solve for x and y:
`x/a + y/b = a + b, x/(a^2)+ y/(b^2) = 2`
Show that the system equations
2x - 3y = 5,
6x - 9y = 15
has an infinite number of solutions
Show that the system of equations
6x + 5y = 11,
9x + 152 y = 21
has no solution.
Find the value of k for which the system of linear equations has an infinite number of solutions:
2x + 3y = 7,
(k – 1)x + (k + 2)y = 3k.
Find the value of k for which the system of linear equations has an infinite number of solutions.
2x + 3y=9,
6x + (k – 2)y =(3k – 2
If 17x + 15y = 11 and 15x + 17y = 21, then find the value of x − y.
