Question

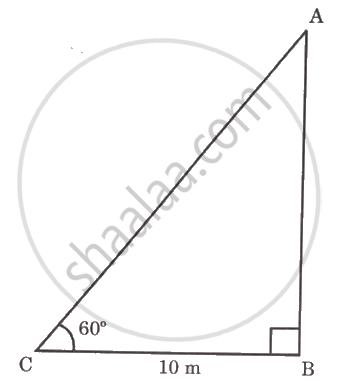
An observer at a distance of 10 m from a tree looks at the top of the tree; the angle of elevation is 60°. To find the height of the tree, complete the activity. `(sqrt3 = 1.73)` 

Activity:

In the figure given above, AB = h = height of tree, BC = 10 m, distance of the observer from the tree. 

Angle of elevation (θ) = ∠BCA = 60°

tan θ = `square/("BC")`  ...(I)

tan 60° = `square`  ...(II)

`("AB")/("BC") = sqrt3`  ...(From (I) and (II))

AB = BC × `sqrt3` = `10sqrt3`

AB = 10 × 1.73 = `square`

∴ Height of the tree is `square` m.

Answer 1

In the figure given above, AB = h = height of tree, BC = 10 m, distance of the observer from the tree. 

Angle of elevation (θ) = ∠BCA = 60°

tan θ = \[\frac{\boxed{\text{AB}}}{\text{BC}}\]  ...(I)

tan 60° = \[\boxed{\sqrt{3}}\]  ...(II)

`("AB")/("BC") = sqrt3`  ...(From (I) and (II))

AB = BC × `sqrt3` = `10sqrt3`

AB = 10 × 1.73 = \[\boxed{17.3}\]

∴ Height of the tree is \[\boxed{17.3}\] m.