Advertisements
Advertisements
प्रश्न
Answer the following in brief.
Calculate the packing efficiency of metal crystal that has simple cubic structure.
उत्तर
Packing efficiency of metal crystal in the simple cubic lattice:
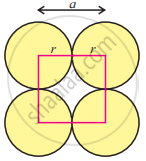
- Step 1: Radius of sphere:
In the simple cubic unit cell, particles (spheres) are at the corners and touch each other along the edge.
A face of a simple cubic unit cell is shown in the figure.
From the figure, we can find that
a = 2r or r = `"a"/2` ......(1)
where, ‘r’ is the radius of atom and ‘a’ is the length of the unit cell edge. - Step 2: Volume of sphere:
Volume of a sphere = `4/3π"r"^3`.
Substitution for r from equation (1) gives:
Volume of one particle = `4/3π ("a"/2)^3` = `(pi"a"^3)/6` ....(2) - Step 3: Total volume of particles:
Because a simple cubic unit cell contains only one particle, the volume occupied by the particle in unit cell =`(pi"a"^3)/6` - Step 4: Packing efficiency:
Packing efficiency = `"Volume occupied by particles in unit cell"/"Total volume of a unit cell" xx 100`
`= (pi"a"^3//6)/"a"^3 xx 100 = (100 pi)/6 = (100 xx 3.142)/6 = 52.36 %`
Thus, in a simple cubic lattice, 52.36 % of total space is occupied by particles and 47.64% is empty space, that is, void volume.
APPEARS IN
संबंधित प्रश्न
Answer the following in brief.
Cesium chloride crystallizes in a cubic unit cell with Cl– ions at the corners and a Cs+ ion in the center of the cube. How many CsCl molecules are there in the unit cell?
Cu crystallizes in fcc unit cell with edge length of 495 pm. What is the radius of Cu atom?
An element has a bcc structure with a unit cell edge length of 288 pm. How many unit cells and a number of atoms are present in 200 g of the element? (1.16 × 1024, 2.32 × 1024)
Calculate the packing efficiency for bcc lattice.
A substance crystallizes in fcc structure. The unit cell edge length is 367.8 pm. Calculate the molar mass of the substance if its density is 21.5 g/cm3.
A compound is formed by elements A and B. This crystallizes in the cubic structure when atoms A are at the comers of the cube and atoms B are at the centre of the body. The simplest formula of the compounds is ____________.
Identify the INCORRECT match.
A compound of X and Y crystallizes in ccp structure in which the X atoms occupy the lattice points at the corners of cube and Y atoms occupy the centres of each of the cube faces. The formula of this compound is ____________.
The number of particles in 1 g of a metallic crystal is equal to ____________.
The vacant space in simple cubic lattice is ____________.
Which of the following contains the highest number of atoms?
The percentage of vacant space of bcc unit cell is ____________.
Which among the following crystal structures the edge length of unit cell is equal to twice the radius of one atom?
What is the edge length of fcc type of unit cell having density and atomic mass 6.22 g cm−3 and 60 g respectively?
Which of the following is INCORRECT?
Copper crystallizes as face centered cubic lattice, with edge length of unit cell 361 pm. Calculate the radius of copper atom.
Copper crystallises with fee unit cell. If the radius of copper atom is 127.8 pm, calculate the density of copper? (At. mass: Cu = 63.55 g mol-1)
What is the percentage of void space in bcc type of in unit cell?
Gold crystallizes in face centred cubic structure. If atomic mass of gold is 197 g mol-1, the mass of unit cell of gold is ______.
The packing efficiency of bcc is ______.
A compound has a hep structure. Calculate the number of voids in 0.4 mol of it.
