Advertisements
Advertisements
प्रश्न
Answer the questions with the help of a given figure.
- State the points which are equidistant from point B.
- Write a pair of points equidistant from point Q.
- Find d(U, V), d(P, C), d(V, B), d(U, L).
Advertisements
उत्तर
(i) The co-ordinates of points B and C are 2 and 4 respectively.
We know that 4 > 2
∴ d(B, C) = 4 − 2
∴ d(B, C) = 2
The co-ordinates of points B and A are 2 and 0 respectively.
We know that 2 > 0
∴ d(B, A) = 2 − 0
∴ d(B, A) = 2
Since d(B, A) = d(B, C), then points A and C are equidistant from point B.
The co-ordinates of points B and D are 2 and 6 respectively.
We know that 6 > 2
∴ d(B, D) = 6 − 2
∴ d(B, D) = 4
The co-ordinates of points B and P are 2 and −2 respectively.
We know that 2 > − 2
∴ d(B, P) = 2 − (− 2)
∴ d(B, P) = 2 + 2
∴ d(B, P) = 4
Since d(B, D) = d(B, P), then points D and P are equidistant from point B.
(ii) The co-ordinates of points Q and U are −4 and −5 respectively.
We know that −4 > −5
∴ d(Q, U) = − 4 − (− 5)
∴ d(Q, U) = − 4 + 5
∴ d(Q, U) = 1
The co-ordinates of points Q and L are −4 and −3 respectively.
We know that − 3 > − 4
∴ d(Q, L) = −3 − (− 4)
∴ d(Q, L) = −3 + 4
∴ d(Q, L) = 1
Since d(Q, U) = d(Q, L), then points U and L are equidistant from point Q.
The co-ordinates of points Q and R are −4 and −6 respectively.
We know that − 4 > − 6
∴ d(Q, R) = −4 − (−6)
∴ d(Q, R) = −4 + 6
∴ d(Q, R) = 2
The co-ordinates of points Q and P are −4 and −2 respectively.
We know that −2 > − 4
∴ d(Q, P) = −2 − (− 4)
∴ d(Q, P) = −2 + 4
∴ d(Q, P) = 2
Since d(Q, R) = d(Q, P), then points R and P are equidistant from point Q.
(iii) The co-ordinates of points U and V are −5 and 5 respectively.
We know that 5 > − 5
∴ d(U, V) = 5 − (− 5)
∴ d(U, V) = 5 + 5
∴ d(U, V) = 10
The co-ordinates of points P and C are −2 and 4 respectively.
We know that 4 > −2
∴ d(P, C) = 4 − (− 2)
∴ d(P, C) = 4 + 2
∴ d(P, C) = 6
The co-ordinates of points V and B are 5 and 2 respectively.
We know that 5 > 2
∴ d(V, B) = 5 − 2
∴ d(V, B) = 3
The co-ordinates of points U and L are −5 and −3 respectively.
We know that − 3 > − 5
∴ d(U, L) = −3 − (−5)
∴ d(U, L) = −3 + 5
∴ d(U, L) = 2
APPEARS IN
संबंधित प्रश्न
The following table shows points on a number line and their co-ordinates. Decide whether the pair of segments given below the table are congruent or not.
| Point | A | B | C | D | E |
| Co-ordinate | -3 | 5 | 2 | -7 | 9 |
seg DE and seg AB
Point P is the midpoint of seg CD. If CP = 2.5, find l(CD).
If AB = 5 cm, BP = 2 cm and AP = 3.4 cm, compare the segments.
How many lines are determined by three distinct points?
Construct a line segment using ruler and compass.
CD = 3.6 cm
The number of line segments in 
is
Name all the line segments in the following figure.
Name the vertices and the line segments in the following figure.
Which points in the following figure appear to be mid-points of the line segments? When you locate a mid-point, name the two equal line segments formed by it.
Is it possible for the same line segment to have two different lengths?
Is it possible for the same angle to have two different measures?
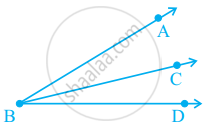
In which of the following figures, perpendicular bisector is shown?
In which of the following figures, only bisector is shown?
In which of the following figures, only perpendicular is shown?
In the following figure how many line segments are there? Name them.
Consider the following figure of line \[\overleftrightarrow{MN}\]. Say whether the following statement is true or false in the context of the given figure.
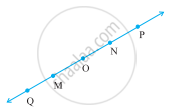
M, O, and N are points on a line segment `overline("MN")`.
A line segment is defined as:
All curved or zig-zag paths between two points are:
