Advertisements
Advertisements
प्रश्न
Can a polyhedron have 10 faces, 20 edges and 15 vertices?
उत्तर
\[\text { No, because every polyhedron satisfies Euler's formula, given below: }\]
\[\text { F+V=E+2 }\]
\[\text { Here, number of faces F = 10 }\]
\[\text { Number of edges E = 20 }\]
\[\text { Number of vertices V = 15 }\]
\[\text { So, by Euler's formula: }\]
\[\text { LHS: 10+15 = 25 }\]
\[\text { RHS: 20 + 2 = 22 }, \]
\[\text { which is not true because 25 }\neq22\]
\[\text { Hence, Eulers formula is not satisfied and no polyhedron may be formed .}\]
APPEARS IN
संबंधित प्रश्न
Can a polyhedron have 10 faces, 20 edges and 15 vertices?
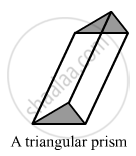
Verify Euler's formula for the following polyhedron:
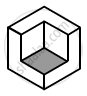
Draw net for the following polyhedron :
If a polyhedron has 10 faces and 8 vertices, find the number of edges in it.
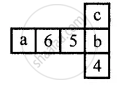
Dice are cubes where the sum of the numbers on the opposite faces is 7. Find the missing numbers a, b and c.
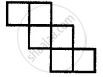
The following figure represent the nets of some solid. Name the solid
Using Euler’s formula, find the unknowns.
| Faces | Verticles | Edges |
| 20 | 10 | ? |
How many vertices does the following solid have?
Tetrahedron
Total number of edges a cylinder has ______.
The corners of solid shapes are called its ______.
