Advertisements
Advertisements
प्रश्न
Cards bearing numbers 3 to 20 are placed in a bag and mixed thoroughly. A card is taken out of the bag at random. What is the probability that the number on the card taken out is an even number?
पर्याय
`9/17`
`1/2`
`5/9`
`7/18`
उत्तर
`bb(1/2)`
Explanation:
Total number of card = 18
n(S) = 18
A = Even numbers from 3 to 20
(A) = 4, 6, 8, 10, 12, 14, 16, 18, 20
n(A) = 9
Required probability P(A) = `(n(A))/(n(S)) = 9/18`
P(A) = `1/2`
APPEARS IN
संबंधित प्रश्न
If S = {2, 4, 6, 8, 10, 12} and A = {4, 8, 12}, find A'
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is neither a heart nor a king
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is Not black
The faces of a red cube and a yellow cube are numbered from 1 to 6. Both cubes are rolled. What is the probability that the top face of each cube will have the same number?
A game consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.
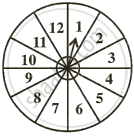
If the outcomes are equally likely, find the probability that the pointer will point at:
- 6
- an even number.
- a prime number.
- a number greater than 8.
- a number less than or equal to 9.
- a number between 3 and 11.
Cards marked with numbers 1, 2, 3 ......... 20 are well shuffled and a card is drawn at random. What is the probability that the number on the card is a prime number?
How many possibilities is following?
Select one card from the pack of 52 cards.
1000 families with 2 children were selected randomly , and the following data were recorded :
| Number of girls in a family | 0 | 1 | 2 |
| Number of families | 333 | 392 | 275 |
Find the probability of a family , having
(iii) no girl
A game consists of spinning an arrow which comes to rest pointing at one of the regions (1, 2 or 3) (figure). Are the outcomes 1, 2 and 3 equally likely to occur? Give reasons.
Assertion (A): The probability that a leap year has 53 Sundays is `2/7`.
Reason (R): The probability that a non-leap year has 53 Sundays is `1/2`.
