Question

Change the order of integration `int_0^aint_sqrt(a^2-x^2)^(x+3a)f(x,y)dxdy`

Answer 1

let I = `int_0^aint_sqrt(a^2-x^2)^(x+3a)f(x,y)dxdy`
Region of integration is : `sqrt(a^2-x^2` ≤𝒚≤ 𝒙+𝟑𝒂
0 ≤𝒙≤𝒂

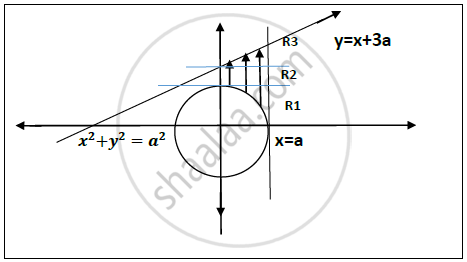
Intersection of x=a and y=x+3a is (a,4a).
Intersection of x=0 and y=x+3a is (0,3a).
Divide the region into three parts R1,R2 and R3
∴ R = R1 ∪𝑹𝟐∪𝑹𝟑
For region R1 : `sqrta^2-y^2 <=x<=a`
                        𝟎≤𝒚≤𝒂
For region R2 : 𝟎≤𝒙≤𝒂
                        𝒂≤𝒚≤𝟑𝒂
For region R3 : (𝒚−𝟑𝒂)≤𝒙≤𝒂
                        3a ≤𝒚≤𝟒𝒂
After changing the order of integration fro dydx to dxdy

`therefore"I"=int_0^aint_(sqrt(a^2-y^2))^af(x,y)dxdy+int_a^(3a)int_0^af(x,y)dxdy+int_(3a)^(4a)int_(y-3a)^4af(x,y)dxdy`