Advertisements
Advertisements
प्रश्न
Consider the situation described in the previous problem. Where should a point source be placed on the principal axis so that the two images form at the same place?
उत्तर
Given,
Convex lens of focal length (fl) = 15 cm
Concave mirror of focal length (fm) = 10 cm
Distance between lens and mirror = 50 cm
Thus, two images will be formed,
(a) One due to direct transmission of light through lens.
(b) One due to reflection and then transmission of the rays through lens.
Let the point source be placed at a distance of 'x' from the lens as shown in the Figure, so that images formed by lens and mirror coincide.
For lens,
We use lens formula:
\[\frac{1}{v} - \frac{1}{u} = \frac{1}{15}\]
\[\Rightarrow v=\frac{15x}{x - 15}...( i)\]
For mirror,
Object distance will be (50 − x)
We use the formula:
\[\frac{1}{v} + \frac{1}{u} = \frac{1}{15}\]
u = − (50 − x)
fm = − 10 cm
\[So, \frac{1}{v_m} + \frac{1}{- (50 - x)} = - \frac{1}{10}\]
\[ \Rightarrow \frac{1}{v_m} = \frac{1}{50 - x} - \frac{1}{10}\]
\[ = \frac{10 - 50 + x}{10(50 - x)}\]
\[ v_m =\frac{x - 40}{10(50 - x)} . . . (ii)\]
Since the distance between lens and mirror is 50 cm,
v − vm = 50
from equation (i) and (ii):
\[\Rightarrow \frac{15x}{x - 15} - \frac{10(50 - x)}{(x - 40)} = 50\]
⇒(3x2 − 120x) − (100x − 2x2 − 1500 + 30x)
= 10 (x2 − 55x + 600)
⇒ 5x2 − 250x − 1500 = 10x2 − 550x + 6000
⇒ 5x2 − 300x + 4500 = 0
⇒ x2 − 60x + 900 = 0
⇒ (x − 30)2 = 0
x = 30 cm.
∴ Point source should be placed at a distance of 30 cm from the lens on the principal axis, so that the two images form at the same place.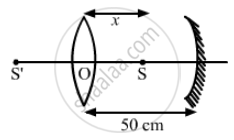
APPEARS IN
संबंधित प्रश्न
Calculate the focal length of a corrective lens having power +2D.
Define the power of a lens.
Define 1 dioptre of power of a lens.
A convex lens forms a real and inverted image of a needle at a distance of 50 cm from it. Where is the needle placed in front of the convex lens if the image is equal to the size of the object? Also, find the power of the lens.
Ranbir claims to have obtained an image twice the size of the object with a concave lens. Is he correct? Give a reason for your answer.
What can you see in a completely dark room? If you switch on an electric bulb in this dark room as a light source, explain how you could now see:
(a) the electric bulb
(b) a piece of white paper
Give the usual name for the following:
A point inside a lens through which the light passes undeviated.
Which has more power : a thick convex lens or a thin convex lens, made of the same glass? Give reason for your choice.
A diverging lens has focal length of 3 cm. Calculate the power.
Two lenses A and B have focal lengths of +20 cm and, −10 cm, respectively.
(a) What is the nature of lens A and lens B?
(b) What is the power of lens A and lens B?
(c) What is the power of combination if lenses A and B are held close together?
Express the power (with sign) of a concave lens of focal length 20 cm.
How does focal length of a lens change when red light incident on it is replaced by violet light? Give reason for your answer.
A double convex lens has focal length 25 cm. The radius of curvature of one of the surfaces is double of the other. Find the radii, if the refractive index of the material of the lens is 1.5.
What is meant by the power of accommodation produced?
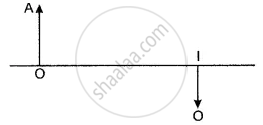
The following diagram shows the object O and the image I formed by a lens. Copy the diagram and on it mark the positions of the lens LL’ and focus (F). Name the lens.
A convex lens is of focal length 20 cm. Find its power.
If focal length of a convex lens is 20 cm at what is the power of the lens?
Power of a lens is – 4D, then its focal length is
Define power of a lens. What is its unit? One student uses a lens of focal length 50 cm and another of –50 cm. What is the nature of the lens and its power used by each of them?
The focal length of a concave lens is 20 cm. The focal length of a convex lens is 25 cm. These two are placed in contact with each other. What is the power of the combination? Is it diverging, converging or undeviating in nature?
