Question

Construct ΔABC, in which ∠B = 70°, ∠C = 60°, AB + BC + AC = 11.2 cm.

Answer 1

Rough figure:

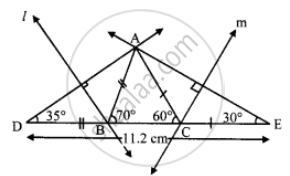
Explanation:

(i) As shown in the figure, take point D and E on line BC, such that

BD = AB and CE = AC     ...(i)

BD + BC + CE = DE      ...[D-B-C, B-C-E]

∴ AB + BC + AC = DE    ...(ii)

Also,

AB + BC + AC= 11.2 cm     ...(iii) [Given]

∴ DE = 11.2 cm        ...[From (ii) and (iii)]

(ii) In ∆ADB

AB = BD       ...[From (i)]

∴ ∠BAD = ∠BDA = x°      ...(iv) [Isosceles triangle theorem]

In ∆ABD, ∠ABC is the exterior angle.

∴ ∠BAD + ∠BDA = ∠ABC      ...[Remote interior angles theorem]

x + x = 70°     ...[From (iv)]

∴ 2x = 70°

∴ x = 35°

∴ ∠ADB = 35°

∴ ∠D = 35°

Similarly, ∠E = 30°

(iii) Now, in ∆ADE

∠D = 35°, ∠E = 30° and DE = 11.2 cm

Hence, ∆ADE can be drawn.

(iv) Since, AB = BD

∴ Point B lies on perpendicular bisector of seg AD.

Also AC = CE

∴ Point C lies on perpendicular bisector of seg AE.

∴ Points B and C can be located by drawing the perpendicular bisector of AD and AE respectively.

∴ ∆ABC can be drawn.

Steps of construction: ​

1. Draw seg DE of length 11.2 cm.
2. From point D draw ray making angle of 35°.
3. From point E draw ray making angle of 30°.
4. Name the point of intersection of two rays as A.
5. Draw the perpendicular bisector of seg DA and seg EA intersecting seg DE in B and C respectively.
6. Join AB and AC.

Therefore, △ABC is the required triangle.