Question

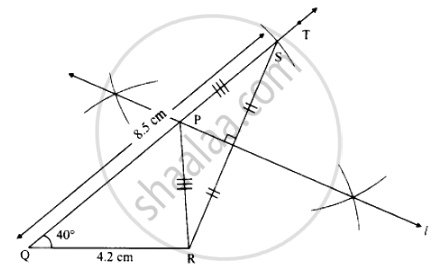
Construct ΔPQR, in which QR = 4.2 cm m∠Q = 40° and PQ + PR = 8.5 cm

Answer 1

Rough figure:

As shown in the rough figure, first we draw seg QR = 4.2 cm of length.

Draw a ray QT making an angle of 40° with seg QR.

Mark point S on QT such that QS = 8.5 cm

Now, QP + PS = QS          ...[Q-P-S]

∴ QP + PS = 8.5 cm          ...(i)

Given PQ + PR = 8.5 cm   ...(ii)

∴ QP + PS = PQ + PR       ...[From (i) and (ii)]

⇒ PS = PR

∴ P is on the perpendicular bisector of SR.

∴ The point of intersection of ray QT and perpendicular bisector of ray SR is point P.

Steps of constructions:

1. Draw seg QR of length 4.2 cm.
2. Draw ray QT such that ∠RQT = 40°.
3. Mark point S on ray QT such that QS = 8.5 cm
4. Draw seg RS.
5. Construct the perpendicular bisector of seg RS.
6. Draw perpendicular bisector of SR which intersects ray QT. Mark the point as P.
7. Draw seg PR.

Therefore, △PQR is the required triangle.