Question

Construct the following and give justification:

A rhombus whose diagonals are 4 cm and 6 cm in lengths.

Answer 1

We know that, all sides of a rhombus are equal and the diagonals of a rhombus are perpendicular bisectors of one another. So, to construct a rhombus whose diagonals are 4 cm and 6 cm use the following steps.

1. Draw the diagonal say AC = 4 cm

2. Taking A and C as centres and radius more than `1/2` AC draw arcs on both sides of the line segment AC to intersect each other.

3. Cut both arcs intersect each other at P and Q, then join PQ.

4. Let PQ intersect AC at the point O. Thus, PQ is perpendicular bisector of AC.

5. Cut off 3 cm lengths from OP and OQ, then we get points B and D.

6. Now, join AB, BC, CD and DA. Thus, ABCD is the required rhombus.

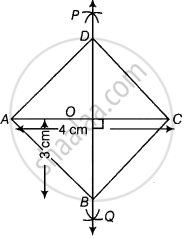
Justification:

Since, D and B lie on perpendicular bisector of AC.

DA = DC and BA = BC   ...(i) [Since, every point on perpendicular bisector of line segment is equidistant from end points of line segment]

Now, ∠DOC = 90°

Also, OD = OB = 3 cm

Thus, AC is perpendicular bisector or BD.

CD = CB  ...(ii)

AB = BC = CD = DA

From equation (i) and (ii)

ABCD is a rhombus.