Advertisements
Advertisements
प्रश्न
Derive an expression for the intensity of electric field at a point in broadside position or on [4)
an equatorial line of an electric dipole.
उत्तर
The electric field at a point, P due to an electric dipole.Due to the positive charge, the positive test charge will experience repulsive force whereas due to negative charge test charge will experience the attraction. Hence,
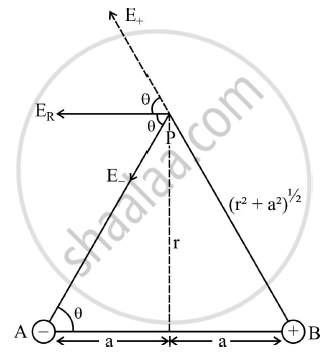
`|E_+| = 1/(4piin_0) q/(r^2 + a^2)`
`|E_-| = 1/(4piin_0) q/(r^2 + a^2)`
`E_R = E_+cos theta + E_- cos theta`
`= 1/(4piin_o) (2q)/(r^2 + a^2) . cos theta`
`= 1/(4piin_0) (2p)/(r^2 + a^2) . (q/(r^2 + a^2)^(1/2))`
`E_R = 1/()4piin_0 (2q xx a)/(r^2 + a^2)^(3/2) = 1/(4piin_0) p/(r^2 + a^2)^(3/2)`
if r >>> a, then
`E_R = 1/(4piin_0) p/r^3`
APPEARS IN
संबंधित प्रश्न
A short electric dipole (which consists of two point charges, +q and -q) is placed at the centre 0 and inside a large cube (ABCDEFGH) of length L, as shown in Figure 1. The electric flux, emanating through the cube is:
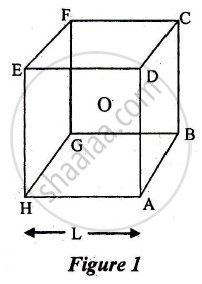
a) `q"/"4piin_9L`
b) zero
c) `q"/"2piin_0L`
d) `q"/"3piin_0L`
(a) Define torque acting on a dipole of dipole moment \[\vec{p}\] placed in a uniform electric field \[\vec{E}\] Express it in the vector from and point out the direction along which it acts.
(c) What would happen if the external field
An electric dipole of length 1 cm, which placed with its axis making an angle of 60° with uniform electric field, experience a torque of \[6\sqrt{3} Nm\] . Calculate the potential energy of the dipole if it has charge ±2 nC.
An electric dipole is placed in an electric field generated by a point charge.
Electric field on the axis of a small electric dipole at a distance r is E1 and at a distance of 2r on its perpendicular bisector, the electric field is E2. Then the ratio E2: E1 is ______.
The ratio of the weight of a man in a stationary lift and in a lift accelerating downwards with a uniform acceleration α is 3 : 2. The acceleration of the lift is:
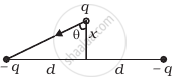
Two charges –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x(x << d) perpendicular to the line joining the two fixed charged as shown in figure. Show that q will perform simple harmonic oscillation of time period.
`T = [(8pi^3 ε_0 md^3)/q^2]^(1/2)`
The electric potential V as a function of distance X is shown in the figure.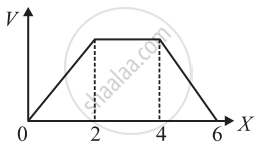
The graph of the magnitude of electric field intensity E as a function of X is ______.
Eight dipoles of charges of magnitude e each are placed inside a cube. The total electric flux coming out of the cube will be ______.
