Advertisements
Advertisements
प्रश्न
Describe briefly:
Arithmetic growth.
उत्तर
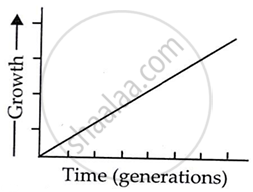
If the length of a plant organ is plotted against time and shows a linear curve, the growth is called arithmetic growth. In this growth, the rate of growth is constant and increase in growth occurs in arithmetic progression.
For example, the length of a plant is measured as 2, 4, 6, 8, 10, or 12 cm at a definite interval of 24 hours. It is found in root or shoots, elongating at constant rate. Arithmetic growth is expressed as Lt = L0 + rt.
Here, Lt = length after time t. L0 = length at the beginning; r = growth rate
APPEARS IN
संबंधित प्रश्न
Define the term growth rate.
Describe briefly:
Geometric growth.
Describe briefly sigmoid growth curve.
Describe briefly:
Absolute and relative growth rates.
Short Answer Question:
Differentiate between Arithmetic and Geometric growth.
Fill in the places with appropriate word/words.
A phase of growth which is maximum and fastest is ______.
A primary root grows from 5 cm to 19 cm in a week. Calculate the growth rate and relative growth rate over the period.
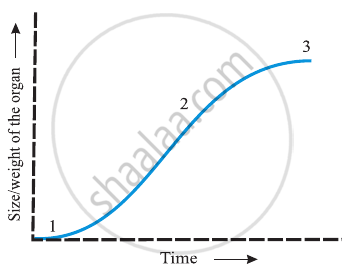
In the figure of Sigmoid growth curve given below, label segments 1, 2 and 3.
Growth is one of the characteristic of all living organisms? Do unicellular organisms also grow? If so, what are the parameters?
Fill in the blanks:
Maximum growth is observed in ______ phase.
