Question

Determine the motional emf induced in a straight conductor rotating in a uniform magnetic field with constant angular velocity about a transverse axis through one end.

Answer 1

Consider the following scenario as seen in the picture, a rod of length l is rotated counterclockwise around an axis that passes through one end and is perpendicular to its length, in a plane perpendicular to a uniform magnetic field of induction `vecB`. `vecB` points into the page. Assume that the rod's constant angular speed is ω.

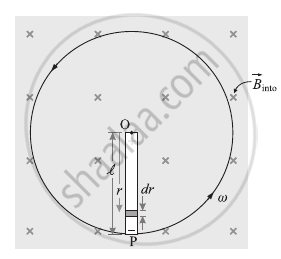
A rod rotating in a uniform magnetic field

Consider an infinitesimal length element dr at a distance r from the rotation axis. In one rotation, the area traced by the element is dA = 2πrdr. Therefore, the time rate at which the element traces out the area is

`(dA)/dt` = frequency of rotation × dA = fdA

where f = `ω/(2π)` is the frequency of rotation.

∴ `(dA)/dt = ω/(2π) (2πrdr) = ωrdr`

Therefore, the magnitude of the induced emf in the element is

`|de| = (dΦ_m)/dt`

= `B(dA)/dt`

= Bωrdr

Since the emfs in all the elements of the rod will be in series, the total emf induced across the ends of the rotating rod is

`|e| = int de`

= `int_0^l Bωrdr`

= `Bω int_0^l rdr`

= `Bω (int^2)/2`

For anticlockwise rotation in `vec (B)` pointing into the page, the pivot point O is at a higher potential.