Advertisements
Advertisements
प्रश्न
Determine the region in the plane determined by the inequalities:
2x + 3y ≤ 35, y ≥ 2, x ≥ 5.
उत्तर
If 2x + 3y = 35 then
| x | 1 | 10 |
| y | 11 | 5 |
y = 2 is a line parallel to X-axis at a distance 2 units
x = 5 is a line parallel to Y-axis at a distance of 5 units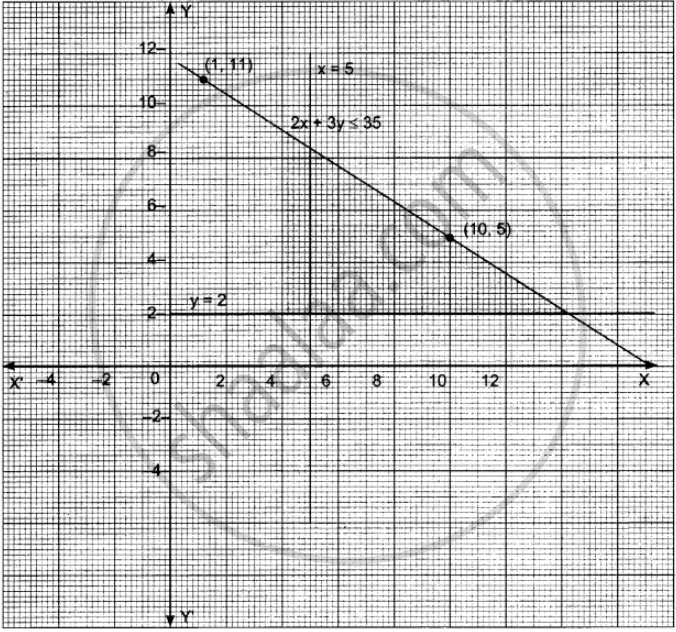
The required region is below 2x + 3y = 35, above y = 2 and to the right of x = 5
APPEARS IN
संबंधित प्रश्न
Find all values of x that satisfies the inequality `(2x - 3)/((x - 2)(x - 4)) < 0`
Resolve the following rational expressions into partial fractions
`1/(x^2 - "a"^2)`
Resolve the following rational expressions into partial fractions
`x/((x - 1)^3`
Resolve the following rational expressions into partial fractions
`1/(x^4 - 1)`
Resolve the following rational expressions into partial fractions
`(x^3 + 2x + 1)/(x^2 + 5x + 6)`
Resolve the following rational expressions into partial fractions
`(x + 12)/((x + 1)^2 (x - 2))`
Resolve the following rational expressions into partial fractions
`(2x^2 + 5x - 11)/(x^2 + 2x - 3)`
Resolve the following rational expressions into partial fractions
`(7 + x)/((1 + x)(1 + x^2))`
Determine the region in the plane determined by the inequalities:
x ≤ 3y, x ≥ y
Determine the region in the plane determined by the inequalities:
y ≥ 2x, −2x + 3y ≤ 6
Determine the region in the plane determined by the inequalities:
3x + 5y ≥ 45, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
x − 2y ≥ 0, 2x − y ≤ −2, x ≥ 0, y ≥ 0
Determine the region in the plane determined by the inequalities:
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
Choose the correct alternative:
The solution of 5x − 1 < 24 and 5x + 1 > −24 is
