Advertisements
Advertisements
प्रश्न
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(y^3 - 3y^2 + 5y - 1) ÷ (y - 1)`
उत्तर
Synthetic Division:
Dividend = `y^3 - 3y^2 + 5y - 1`
Divisor = y − 1
Opposite of −1 = 1
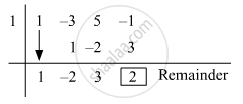
The coefficient form of the quotient is (1, −2, 3).
∴ Quotient = y2 − 2y + 3 and Remainder = 2
Linear Method:
`y^3 - 3y^2 + 5y - 1`
`= y^2 (y - 1) + y^2 - 3y^2 + 5y - 1`
`= y^2 (y - 1) - 2y (y - 1) -2y +5y - 1`
`= y^2 (y - 1) - 2y (y - 1) + 3(y -1) + 3 - 1`
`= (y - 1) (y^2 - 2y + 3) + 2`
APPEARS IN
संबंधित प्रश्न
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(2m^2 - 3m + 10) ÷ (m - 5)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(2x^4 + 3x^3 + 4x - 2x^2) ÷ (x + 3)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(x^4 - 3x^2 - 8) ÷ (x + 4)`
Divide polynomial 3x3 - 8x2 + x + 7 by x - 3 using synthetic method and write the quotient and remainder.
Find the quotient and remainder for the following using synthetic division:
(x3 + x2 – 7x – 3) ÷ (x – 3)
Find the quotient and remainder for the following using synthetic division:
(x3 + 2x2 – x – 4) ÷ (x + 2)
Find the quotient and remainder for the following using synthetic division:
(3x3 – 2x2 + 7x – 5) ÷ (x + 3)
If the quotient obtained on dividing (8x4 – 2x2 + 6x – 7) by (2x + 1) is (4x3 + px2 – qx + 3), then find p, q and also the remainder
Factorise the following polynomials using synthetic division:
– 7x + 3 + 4x3
Factorise the following polynomials using synthetic division:
x3 + x2 – 14x – 24
