Advertisements
Advertisements
प्रश्न
Divide. Write the quotient and the remainder.
40a3 ÷ (−10a)
उत्तर
40a3 ÷ (−10a)
\[= \frac{40 a^3}{\left( - 10a \right)}\]
\[ = \frac{\left( - 4 \right) \times \left( - 10a \right) \times a^2}{\left( - 10a \right)}\]
\[ = - 4 a^2\]
So, quotient = \[- 4 a^2\] and remainder = 0
संबंधित प्रश्न
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`x+x^2 +4`
Write the standard form of a cubic polynomial with real coefficients.
If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeros are coincident. (True/False).
If f(x) is a polynomial such that f(a) f(b) < 0, then what is the number of zeros lying between a and b?
If the product of zeros of the polynomial f(x) ax3 − 6x2 + 11x − 6 is 4, then a =
Divide. Write the quotient and the remainder.
40m5 ÷ 30m3
Case Study -1

The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time‘t’ in seconds is given by the polynomial h(t) such that h(t) = -16t2 + 8t + k.
What is the value of k?
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.


The shape of the poses shown is:
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

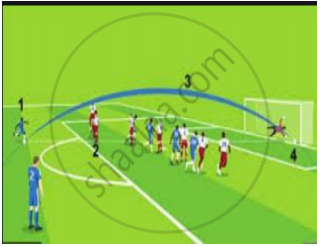
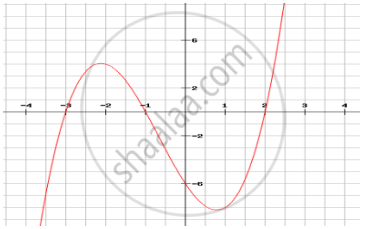
The three zeroes in the below shown graph are:
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the degree of the polynomial
