Question

Draw a ray diagram for the formation of the image of an object by a convex mirror. Hence, obtain the mirror equation.

Answer 1

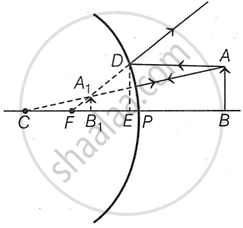
Let AB be an object placed on the principal axis of a convex mirror of focal length f; u is the distance between the object and the mirror, and v is the distance between the image and mirror.

In ΔABC and ΔA₁B₁C

∠ABC = ∠A₁B₁C   ...(right angles)

∠ACB = ∠A₁CB₁   ...(common angle)

∴ ∠CAB = ∠CA₁B

∴ ΔABC is similar to ΔA₁B₁C

`therefore (AB)/(A_1B_1) = (BC)/(B_1C)`   ...(i)

Similarly, ΔDEF is similar to ΔA₁B₁F

`therefore (DE)/(A_1B_1) = (EF)/(B_1F)`   ...(ii)

But DE = AB and when the aperture is very small = EF = PF

Eq. (ii) becomes

`(AB)/(A_1B_1) = (PF)/(B_1F)`   ...(iii)

From Eqs. (i) and (iii), we get

`(PF)/(B_1F) = (BC)/(B_1C)`

= `(PF)/(PF - PB_1) = (PB + BC)/(PC - PB_1)`

= `f/(f - v) = (-u + 2f)/(2f - v)`

Since PF = F, PB₁ = v, PB = u, PC = 2f

⇒ 2(2f − v) = (f − v)(2f − u)

⇒ 2f² − vf = 2f² − uf − 2fv + uv = 0

⇒ 2f² − vf − 2f² + uf + 2fv − uv = 0

⇒ − vf + uf + 2fv − vu = 0

fv + uf − vu = 0   ...(iv)

Dividing both sides of the Eq. (iv) by uvf, we get

⇒ `(fv)/(uvf) + (uf)/(uvf) - (vu)/(uvf) = 0`

⇒ `1/v + 1/u = 1/f`