Advertisements
Advertisements
प्रश्न
Draw at least three different nets for making a cube.
उत्तर
(i)
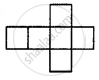
(ii)
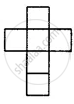
(iii)
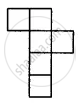
संबंधित प्रश्न
Can a polyhedron have for its faces a square and four triangles?
Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid).
The given Figure are prisms or not?
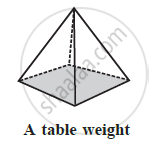
How are prisms and cylinders alike?
How are pyramids and cones alike?
Is a square prism same as a cube? Explain.
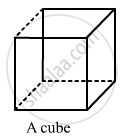
Verify Euler’s formula for given solids.
Using Euler’s formula, find the unknown.
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
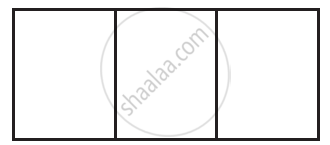
Here is an incomplete net for making a cube. Complete it in at least two different ways. Remember that a cube has six faces. How many are there in the net here? (Give two separate diagrams. If you like, you may use a squared sheet for easy manipulation.)
Can a polyhedron have for its face 3 triangles?
Can a polyhedron have for its face a square and four triangles?
Is it possible to have a polyhedron with any given number of faces?
Name the polyhedron that can be made by folding net:
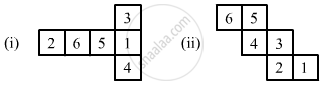
Dice are cubes where the numbers on the opposite faces must total 7. Which of the following are dice?
Draw net for the following polyhedron :
Dice are cubes where the sum of the numbers on the opposite faces is 7. Find the missing numbers a, b and c.
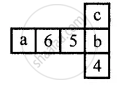
Dice are cubes with dots or dots on the face. Opposite faces of a die always have a total of seven on them.
In the given below net to make dice (cube), the numbers inserted in the square indicate the number of dots in it.
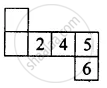
Insert suitable numbers in the blank so that numbers in opposite faces of the die have a total of seven dots.
The following figure, given below, shows shadows of some 3D object when seen under the lamp of an overhead projector:
Verify Euler’s formula for the table given below.
| Faces | Verticles | Edges |
| 12 | 20 | 30 |
Verify Euler’s formula for the table given below.
| Faces | Vertices | Edges |
| 32 | 60 | 90 |
Using Euler’s formula, find the unknowns.
| Faces | Verticles | Edges |
| 20 | 10 | ? |
In the figure,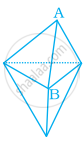 
the number of faces meeting at B is ______.
How many vertices does the following solid have?
Cylinder
How many vertices does the following solid have?
Octagonal Pyramid
How many edges does the following solid have?
Octagonal Pyramid
Find the number of faces in the given shape:
