Advertisements
Advertisements
प्रश्न
एक दी हुई किरण के प्रारंभिक बिंदु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
उत्तर
45° का कोण बनाने के लिए नीचे दिए गए चरणों का पालन किया जाएगा।
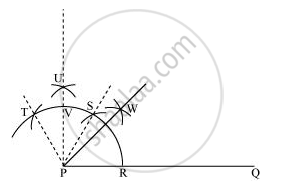
(i) दी गई किरण PQ लीजिए। बिंदु P को अपना केंद्र मानकर किसी त्रिज्या का एक चाप खींचिए जो PQ को R पर काटता है।
(ii) R को केंद्र मानकर और पहले की समान त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को S पर काटता है।
(iii) S को केंद्र मानकर और उसी त्रिज्या से जो पहले थी, एक चाप खींचिए जो चाप को T पर काटता है (आकृति देखिए)।
(iv) S और T को केंद्र मानकर एक दूसरे को U पर प्रतिच्छेद करने के लिए समान त्रिज्या का एक चाप खींचिए।
(v) PU में शामिल हों। मान लीजिए यह चाप को बिंदु V पर काटती है।
(vi) R और V से, 1/2RV से अधिक त्रिज्या वाले चाप खींचिए जो एक दूसरे को W पर काटेंगे। PW को मिलाइए।
PQ के साथ 45° बनाने वाली आवश्यक किरण PW है।

निर्माण का औचित्य:
यदि हम ∠WPQ = 45° सिद्ध कर सकते हैं, तो हम रचना का औचित्य सिद्ध कर सकते हैं।
इसके लिए PS और PT को ज्वाइन करें।
हमारे पास है, ∠SPQ = ∠TPS = 60° इस निर्माण के (iii) और (iv) चरणों में, PU को के द्विभाजक के रूप में तैयार किया गया था ∠TPS.
∴ ∠UPS = 1/2 ∠TPS = 60°/2 = 30°
भी, ∠UPQ = ∠SPQ + ∠UPS
= 60° + 30°
= 90°
इस निर्माण के चरण (vi) में, पीडब्लू का निर्माण के द्विभाजक के रूप में किया गया था ∠UPQ.
∴ ∠WPQ = 1/2 ∠UPQ = 90°/2 = 45°
APPEARS IN
संबंधित प्रश्न
निम्न माप के कोण की रचना कीजिए:- 30°
75° के कोणों की रचना कीजिए और इसे एक चांदे से मापकर सत्यापित कीजिए।
135° के कोणों की रचना कीजिए और इसे एक चांदे से मापकर पुष्टि कीजिए।
42.5° के कोण की रचना की जा सकती है।
एक त्रिभुज ABC की रचना की जा सकती है, जिसमें AB = 5 cm, ∠A = 45° और BC + AC = 5 cm है।
एक त्रिभुज ABC की रचना की जा सकती है, जिसमें ∠B = 105°, ∠C = 90° और AB + BC + AC = 10 cm है।
4 cm लंबाई का एक रेखाखंड खींचिए। क्रमश : A और B से होकर, AB पर लंब रेखाएँ खींचिए। क्या ये रेखाएँ समांतर हैं?
चाँदे की सहायता से 80° का एक कोण खींचिए। 40°, 160° और 120° के कोणों की रचना कीजिए।
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 5 cm, ∠B = 60° और AC + AB = 7.5 cm है।
3 cm भुजा वाले एक वर्ग की रचना कीजिए।
